题目内容
设定义在(0,+∞)上的函数f(x)=ax+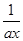 +b(a>0).
+b(a>0).
(1)求f(x)的最小值;
(2)若曲线y=f(x)在点(1,f(1))处的切线方程为y=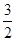 x,求a,b的值.
x,求a,b的值.
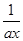 +b(a>0).
+b(a>0).(1)求f(x)的最小值;
(2)若曲线y=f(x)在点(1,f(1))处的切线方程为y=
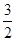 x,求a,b的值.
x,求a,b的值.(1)b+2(2)a=2,b=-1
(1)f(x)=ax+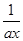 +b≥2
+b≥2 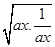 +b=b+2,
+b=b+2,
当且仅当ax=1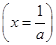 时,f(x)取得最小值为b+2.
时,f(x)取得最小值为b+2.
(2)由题意得:f(1)=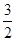 ?a+
?a+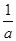 +b=
+b=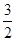 ,①
,①
f′(x)=a-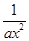 ⇒f′(1)=a-
⇒f′(1)=a-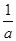 =
=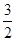 ,②
,②
由①②得:a=2,b=-1.
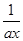 +b≥2
+b≥2 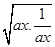 +b=b+2,
+b=b+2,当且仅当ax=1
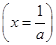 时,f(x)取得最小值为b+2.
时,f(x)取得最小值为b+2.(2)由题意得:f(1)=
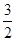 ?a+
?a+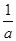 +b=
+b=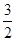 ,①
,①f′(x)=a-
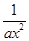 ⇒f′(1)=a-
⇒f′(1)=a-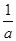 =
=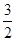 ,②
,②由①②得:a=2,b=-1.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
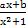 在点(-1,f(-1))处的切线方程为x+y+3=0.
在点(-1,f(-1))处的切线方程为x+y+3=0.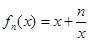 ,(
,(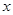 >0,
>0,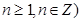 ,以点
,以点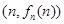 为切点作函数
为切点作函数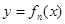 图象的切线
图象的切线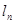 ,记函数
,记函数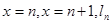 所围成的区域面积为
所围成的区域面积为 .
.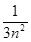 ;
;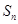 为数列
为数列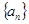 的前
的前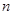 项和,求证:
项和,求证: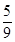 .来
.来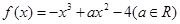 .
.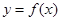 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为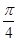 ,求
,求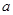 的值;
的值;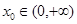 使
使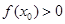 ,求
,求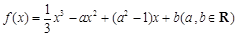
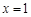 为
为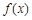 的极值点,求
的极值点,求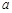 的值;
的值;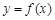 的图象在点
的图象在点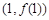 处的切线方程为
处的切线方程为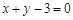 ,
,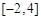 上的最大值;
上的最大值;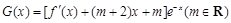 的单调区间.
的单调区间.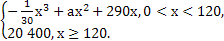
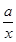 +ln x-1.
+ln x-1.