题目内容
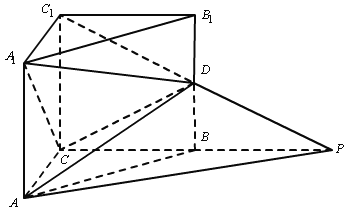
【题目】如图:在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上一点,
上一点,![]() 是
是![]() 的延长线与
的延长线与![]() 的延长线的交点,且
的延长线的交点,且![]() 平面
平面![]() .
.
(1)求证:![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)若点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连结![]() ,设
,设![]() ,连结
,连结![]() ,由
,由![]() 平面
平面![]() ,利用线面平行的性质,可得
,利用线面平行的性质,可得![]() ,由
,由![]() 是
是![]() 的中点,证得
的中点,证得![]() 为
为![]() 的中点;
的中点;
(2)建立空间直角坐标系,用向量法求二面角![]() 的正弦值;
的正弦值;
(3)在第二问的基础上,设![]() ,根据直线
,根据直线![]() 与平面
与平面![]() 所成的角的正弦值,求出
所成的角的正弦值,求出![]() ,求出线段
,求出线段![]() 的长
的长
(1)连结![]() ,设
,设![]() ,连结
,连结![]()
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() 为正方形
为正方形![]() 的中心,∴
的中心,∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .
.
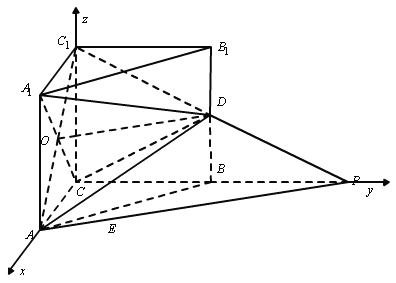
(2)以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,又
,又![]()
则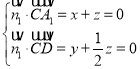 ,令
,令![]() ,得
,得![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,又
,又![]()
则则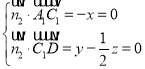 ,令
,令![]() ,得
,得![]() ,
,
∴ .
.
∴![]() .
.
∴二面角![]() 的正弦值为
的正弦值为![]() .
.
(3)设![]() ,其中
,其中![]()
∴![]()
∵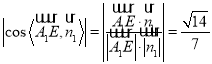 ,∴
,∴![]()
∴![]() ,
,![]() .
.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案【题目】在我国,大学生就业压力日益严峻,伴随着政府政策引导与社会观念的转变,大学生创业意识,就业方向也悄然发生转变某大学生在国家提供的税收,担保贷款等很多方面的政策扶持下选择加盟某专营店自主
创业,该专营店统计了近五年来创收利润数![]() (单位:万元)与时间
(单位:万元)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 2.4 | 2.7 | 4.1 | 6.4 | 7.9 |
(Ⅰ)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合):
,则线性相关程度很高,可用线性回归模型拟合):
(Ⅱ)该专营店为吸引顾客,特推出两种促销方案.
方案一:每满500元可减50元;
方案二:每满500元可抽奖一次,每次中奖的概率都为![]() ,中奖就可以获得100元现金奖励,假设顾客每次抽奖的结果相互独立.
,中奖就可以获得100元现金奖励,假设顾客每次抽奖的结果相互独立.
①某位顾客购买了1050元的产品,该顾客选择参加两次抽奖,求该顾客获得100元现金奖励的概率.
②某位顾客购买了1500元的产品,作为专营店老板,是希望该顾客直接选择返回150元现金,还是选择参加三次抽奖?说明理由
附:相关系数公式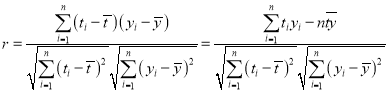
参考数据:![]() .
.
【题目】2019年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善生存环境质量.某部门在某小区年龄处于区间![]() 内的人中随机抽取
内的人中随机抽取![]() 人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
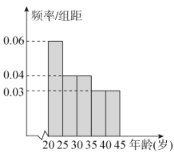
(1)求![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
(3)从年龄段在![]() 的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间
的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间![]() 中的概率.
中的概率.
组数 | 分组 | “环保族”人数 | 占本组频率 |
第一组 |
| 45 | 0.75 |
第二组 |
| 25 |
|
第三组 |
|
| 0.5 |
第四组 |
| 3 | 0.2 |
第五组 |
| 3 | 0.1 |