题目内容
1.已知f(x)=ln(x2+2016)+|2015x|,当f(2m-1)>f(m-1),则m的取值范围是( )| A. | m>0 | B. | m<0 | C. | m$>\frac{2}{3}$或m<0 | D. | m>1 |
分析 根据题意得f(x)是定义域R上的偶函数,且x≤0时f(x)是减函数,x>0时f(x)是增函数;由此把f(2m-1)>f(m-1)化为|2m-1|>|m-1|,从而求出m的取值范围.
解答 解:∵f(x)=ln(x2+2016)+|2015x|,
∴f(-x)=f(x),
∴f(x)是定义域R上的偶函数,
且x≤0时f(x)是减函数,x>0时f(x)是增函数;
∴当f(2m-1)>f(m-1)时,
有|2m-1|>|m-1|,
即4m2-4m+1>m2-2m+1,
化简得3m2-2m>0,
解得m<0或m>$\frac{2}{3}$;
∴m的取值范围是m<0或m>$\frac{2}{3}$.
故选:C.
点评 本题考查了函数的奇偶性与单调性的应用问题,也考查了转化思想以及不等式的解法与应用问题,是综合性题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知x,y满足条件$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,则z=$\frac{x+y+2}{x+3}$的最小值( )
| A. | -$\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{13}{6}$ | D. | 4 |
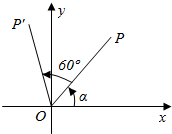 如图,保持点P(3,3)与原点的距离不变,并绕原点旋转60°到P′位置,设点P′的坐标为(x′,y′).
如图,保持点P(3,3)与原点的距离不变,并绕原点旋转60°到P′位置,设点P′的坐标为(x′,y′).