题目内容
16.已知数列{an}的通项an=2n+1,由bn=$\frac{{a}_{1}+{a}_{2}+{a}_{3}+…+{a}_{n}}{n}$所确定的数列{bn}的前n项和是Sn=$\frac{1}{2}{n}^{2}$+$\frac{5}{2}n$.分析 数列{an}的通项an=2n+1,利用等差数列的前n项和公式可得:其前n项和Sn=n2+2n.于是bn=$\frac{{a}_{1}+{a}_{2}+{a}_{3}+…+{a}_{n}}{n}$=n+2.再利用等差数列的前n项和公式即可得出.
解答 解:∵数列{an}的通项an=2n+1,
∴其前n项和Sn=$\frac{n(3+2n+1)}{2}$=n2+2n.
∴bn=$\frac{{a}_{1}+{a}_{2}+{a}_{3}+…+{a}_{n}}{n}$=n+2.
∴数列{bn}的前n项和Sn=$\frac{n(3+n+2)}{2}$=$\frac{1}{2}{n}^{2}$+$\frac{5}{2}n$.
故答案为:$\frac{1}{2}{n}^{2}$+$\frac{5}{2}n$.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
5.下列四个函数:①y=$\frac{x}{x-1}$;②y=x2+x;③y=-(x+1)2;④y=$\frac{x}{1-x}$+2,其中在(-∞,0)上为减函数的是( )
| A. | ① | B. | ④ | C. | ①④ | D. | ①②④ |
1.已知f(x)=ln(x2+2016)+|2015x|,当f(2m-1)>f(m-1),则m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m$>\frac{2}{3}$或m<0 | D. | m>1 |
8.曲线${∫}_{-\sqrt{2}}^{2}$(-$\sqrt{2-{x}^{2}}$)dx( )
| A. | -2π | B. | -π | C. | 2π | D. | π |
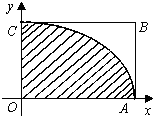 如图,曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1(0≤x≤3,0≤y≤2),为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积,现采用随机模拟方式产生x∈(0,3),y∈(0,2)的200个点(x,y),经统计,落在图中阴影部分的点共157个,则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84.(精确到0.01)
如图,曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1(0≤x≤3,0≤y≤2),为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积,现采用随机模拟方式产生x∈(0,3),y∈(0,2)的200个点(x,y),经统计,落在图中阴影部分的点共157个,则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84.(精确到0.01)