题目内容
已知函数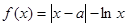
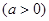 .
.
(1)若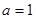 ,求
,求 的单调区间及
的单调区间及 的最小值;
的最小值;
(2)若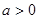 ,求
,求 的单调区间;
的单调区间;
(3)试比较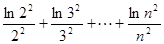 与
与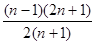 的大小
的大小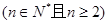 ,并证明你的结论.
,并证明你的结论.
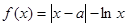
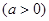 .
.(1)若
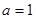 ,求
,求 的单调区间及
的单调区间及 的最小值;
的最小值;(2)若
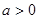 ,求
,求 的单调区间;
的单调区间;(3)试比较
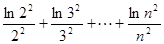 与
与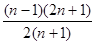 的大小
的大小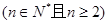 ,并证明你的结论.
,并证明你的结论.(1)0
(2)当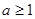 时,
时,  的递增区间是
的递增区间是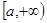 ,递减区间是
,递减区间是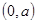 ;
;
当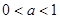 ,
, 的递增区间是
的递增区间是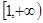 ,递减区间是
,递减区间是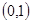
(3)根据题意,由于由(1)可知,当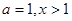 时,有
时,有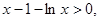 即
即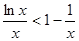 ,那么利用放缩法来证明。
,那么利用放缩法来证明。
(2)当
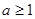 时,
时,  的递增区间是
的递增区间是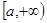 ,递减区间是
,递减区间是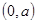 ;
;当
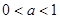 ,
, 的递增区间是
的递增区间是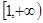 ,递减区间是
,递减区间是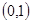
(3)根据题意,由于由(1)可知,当
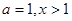 时,有
时,有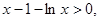 即
即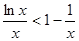 ,那么利用放缩法来证明。
,那么利用放缩法来证明。试题分析:(1) 当
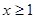 时,
时,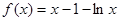 ,
,
 在
在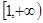 上是递增.
上是递增.当
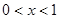 时,
时,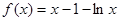 ,
,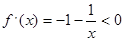 .
. 在
在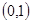 上是递减.
上是递减.故
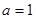 时,
时,  的增区间为
的增区间为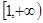 ,减区间为
,减区间为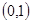 ,
, . 4分
. 4分(2) ①若
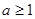 ,
,当
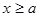 时,
时,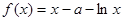 ,
,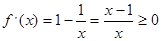 ,则
,则 在区间
在区间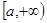 上是递增的;
上是递增的;当
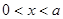 时,
时,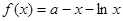 ,
, 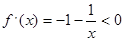 ,则
,则 在区间
在区间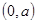 上是递减的 6分
上是递减的 6分②若
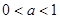 ,
,当
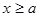 时,
时, 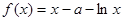 ,
, 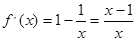 ,
, ;
;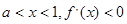 . 则
. 则 在
在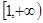 上是递增的,
上是递增的,  在
在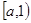 上是递减的;
上是递减的; 当
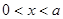 时,
时,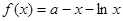 ,
, 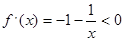
 在区间
在区间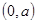 上是递减的,而
上是递减的,而 在
在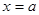 处有意义;
处有意义; 则
 在区间
在区间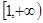 上是递增的,在区间
上是递增的,在区间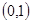 上是递减的 8分
上是递减的 8分综上: 当
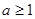 时,
时,  的递增区间是
的递增区间是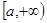 ,递减区间是
,递减区间是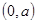 ;
;当
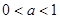 ,
, 的递增区间是
的递增区间是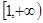 ,递减区间是
,递减区间是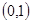 9分
9分(3)由(1)可知,当
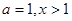 时,有
时,有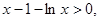 即
即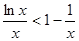
则有
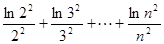

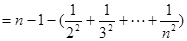 12分
12分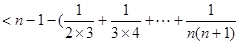
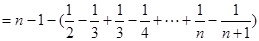
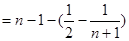 =
=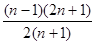
故:
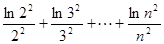
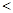
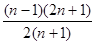 . 15分
. 15分点评:主要是考查了导数在研究函数单调性,以及函数最值方面的运用,属于中档题。

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
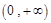 上单调递增的函数是( )
上单调递增的函数是( )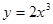
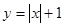
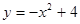
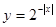
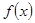 对于任意的
对于任意的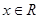 ,导函数
,导函数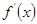 都存在,且满足
都存在,且满足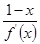 ≤0,则必有( )
≤0,则必有( )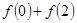 >
>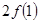
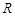 上的函数
上的函数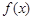 满足
满足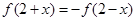 ,当
,当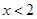 时,
时,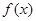 单调递增,若
单调递增,若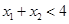 且
且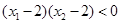 ,则
,则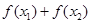 的值( )
的值( )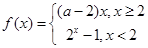 满足对任意实数
满足对任意实数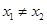 ,都有
,都有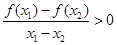 成立,则实数
成立,则实数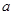 的取值范围为( )
的取值范围为( )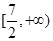
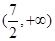
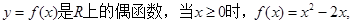
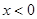 时,函数
时,函数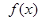 的表达式;
的表达式; 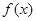 的图象,并指出其单调区间。
的图象,并指出其单调区间。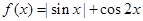 ,若
,若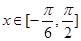 则函数
则函数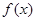 的最小值是 ( )
的最小值是 ( )
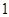
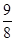
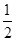
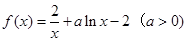 .
.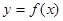 在点
在点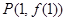 处的切线与直线
处的切线与直线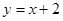 垂直,求函数
垂直,求函数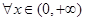 都有
都有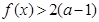 成立,试求
成立,试求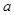 的取值范围;
的取值范围;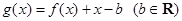 .当
.当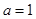 时,函数
时,函数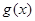 在区间
在区间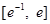 上有两个零点,求实数
上有两个零点,求实数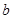 的取值范围.
的取值范围.