题目内容
【题目】已知向量 
=（1，sinx）， 
=（cos（2x+ 
），sinx），函数f（x）= ﹣ 
cos2x
（1）求函数f（x）的解析式及其单调递增区间；
（2）当x∈[0， ]时，求函数f（x）的值域．
【答案】
（1）解：函数f（x）= 
﹣ 
cos2x
=cos2xcos 
﹣sin2xsin 
= 
，
由2k 
，
可得k 
，
单调递增区间为：[k 
， 
]
（2）解：当x∈[0， ]时，
可得2x 
，
因此sin（2x+ 
） 
，
所以函数f（x）的值域是 
【解析】（1）首先根据 =（1，sinx）， =（cos（2x+ ），sinx），求出 
；然后根据函数f（x）= ﹣ cos2x，求出函数f（x）的解析式；最后根据正弦函数的特征，求出其单调递增区间即可；（2）当x∈[0， ]时，可得2x ，然后求出函数f（x）的值域即可．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某车间为了规定工时定额，需要确定加工零件所花费的时间，为此做了四次试验，得到的数据如表：
零件的个数x（个） | 2 | 3 | 4 | 5 |
加工的时间y（小时） | 2.5 | 3 | 4 | 4.5 |
（1）求出y关于x的线性回归方程 
；
（2）试预测加工10个零件需要多少小时？
（参考公式： 
= 
= 
； 
；）
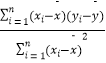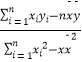