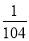题目内容
2.已知数列{an}中,a1=1,a1+2a2+3a3+…+nan=$\frac{n+1}{2}$an+1(Ⅰ)求数列{an}的通项an;
(Ⅱ)求数列{n2an}的前n项和Tn;
(Ⅲ)若存在n∈N*,使得an≤(n+1)λ成立,求实数λ的最小值.
分析 (Ⅰ)将n换为n-1,相减可得n≥2时,数列{nan}是以2为首项,3为公比的等比数列,由等比数列的求和公式即可得到所求;
(Ⅱ)由(Ⅰ)可知当n≥2时,${n^2}{a_n}=2n•{3^{n-2}}$,运用错位相减法,即可得到所求;
(Ⅲ)若存在n∈N*,使得an≤(n+1)λ成立,即为λ≥$\frac{{a}_{n}}{n+1}$,令f(n)=$\frac{2•{3}^{n-2}}{n(n+1)}$,判断单调性,可得f(n)的最小值,由存在性问题的解法,可得实数λ的最小值.
解答 解:(Ⅰ)∵${a_1}+2{a_2}+3{a_3}+…+n{a_n}=\frac{n+1}{2}{a_{n+1}}$,n∈N*①
∴${a_1}+2{a_2}+3{a_3}+…+(n-1){a_n}=\frac{n}{2}{a_n}$,n≥2②,
①-②:$n{a_n}=\frac{n+1}{2}{a_{n+1}}-\frac{n}{2}{a_n}$,
∴$\frac{3n}{2}{a_n}=\frac{n+1}{2}{a_{n+1}}$,
即(n+1)an+1=3nan(n≥2),
又2a2=2a1=2,
∴n≥2时,数列{nan}是以2为首项,3为公比的等比数列.
∴$n{a_n}=2•{3^{n-2}}(n≥2)$,
故${a_n}=\left\{\begin{array}{l}1\;,n=1\\ \frac{2}{n}•{3^{n-2}}\;,n≥2\end{array}\right.$;
(Ⅱ)由(Ⅰ)可知当n≥2时,${n^2}{a_n}=2n•{3^{n-2}}$,∴当n=1时,T1=1;
当n≥2时,${T_n}=1+4•{3^0}+6•{3^1}+…+2n•{3^{n-2}}$,①$3{T_n}=3+4•{3^1}+6•{3^2}+…+2(n-1)•{3^{n-2}}+2n•{3^{n-1}}$,②
①-②得,$-2{T_n}=2+2({3^1}+{3^2}+…+{3^{n-2}})-2n•{3^{n-1}}$
=2-3+3n-1-2n•3n-1=-1+(1-2n)•3n-1
∴${T_n}=\frac{1}{2}+(n-\frac{1}{2}){3^{n-1}}(n≥2)$,又T1=1也满足,
∴${T_n}=\frac{1}{2}+(n-\frac{1}{2}){3^{n-1}}(n∈{N^*})$.
(Ⅲ)若存在n∈N*,使得an≤(n+1)λ成立,即为λ≥$\frac{{a}_{n}}{n+1}$,
当n≥2时,λ≥$\frac{2•{3}^{n-2}}{n(n+1)}$,
令f(n)=$\frac{2•{3}^{n-2}}{n(n+1)}$
,则$\frac{f(n+1)}{f(n)}$=$\frac{2•{3}^{n-1}}{(n+1)(n+2)}$•$\frac{n(n+1)}{2•{3}^{n-2}}$=3n>1,
又f(n)>0,即有f(n+1)>f(n),当n≥2时,f(n)单调递增,
f(n)的最小值为f(2)=$\frac{1}{3}$,
而n=1时,$\frac{{a}_{1}}{1+1}$=$\frac{1}{2}$,综上可得$\frac{{a}_{n}}{n+1}$的最小值为$\frac{1}{3}$.
即有λ≥$\frac{1}{3}$,即实数λ的最小值为$\frac{1}{3}$.
点评 本题考查数列的通项的求法和数列求和的方法:错位相减法,考查等比数列的通项和求和公式的运用,考查不等式成立问题的解法,属于中档题.

| A. | 15 | B. | 25 | C. | 35 | D. | 50 |
| A. | (0,$\frac{\sqrt{2}}{2}$]∪[4,+∞) | B. | [$\frac{\sqrt{2}}{2}$,1)∪(1,4] | C. | ($\frac{\sqrt{2}}{2}$,1)∪(1,4) | D. | (0,$\frac{\sqrt{2}}{2}$)∪(4,+∞) |
| A. | 4 | B. | 14 | C. | 16 | D. | 18 |
| A. | -2,-3 | B. | -3,-6 | C. | -2,-6 | D. | 0,-2 |
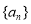 中,
中,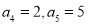 ,则数列
,则数列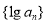 的前8项和等于
的前8项和等于 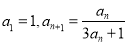 ,则给出的数列{
,则给出的数列{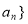 第34项( )
第34项( )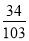 B.
B.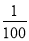 C.100 D.
C.100 D.