题目内容
7.已知函数y=$\frac{1}{x}$($\frac{1}{2}$≤x≤2)的图象与函数y=ax(a>0且a≠1)的图象有一个交点,则实数a的取值范围是( )| A. | (0,$\frac{\sqrt{2}}{2}$]∪[4,+∞) | B. | [$\frac{\sqrt{2}}{2}$,1)∪(1,4] | C. | ($\frac{\sqrt{2}}{2}$,1)∪(1,4) | D. | (0,$\frac{\sqrt{2}}{2}$)∪(4,+∞) |
分析 作函数y=$\frac{1}{x}$($\frac{1}{2}$≤x≤2)与函数y=ax(a>0,a≠1)的图象,利用数形结合的方法求解即可.
解答  解:作函数y=$\frac{1}{x}$($\frac{1}{2}$≤x≤2)与函数y=ax(a>0,a≠1)的图象,
解:作函数y=$\frac{1}{x}$($\frac{1}{2}$≤x≤2)与函数y=ax(a>0,a≠1)的图象,
结合图象可知,当0<a<1时,a2≥$\frac{1}{2}$,
解得$\frac{\sqrt{2}}{2}$≤a<1;
当a>1时,${a}^{\frac{1}{2}}$≤2,
解得1<a≤4.
综上可得,$\frac{\sqrt{2}}{2}$≤a<1或1<a≤4.
故选:B.
点评 本题考查了学生的作图与应用图象的能力,同时考查了指数函数的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.一物体的运动方程为s=t2-t+5,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )
| A. | 7米/秒 | B. | 6米/秒 | C. | 5米/秒 | D. | 8米/秒 |
16.过点P(3,0)有一条直线l,它夹在两条直线l1:2x-y-2=0与l2:x+y+3=0之间的线段恰被点P平分,则直线l方程为( )
| A. | 6x-y-18=0 | B. | 8x-y-24=0 | C. | 5x-2y-15=0 | D. | 8x-3y-24=0 |
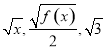 (x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).
(x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).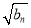 是
是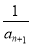 ,
, 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn. 中,已知
中,已知  ,则S21等于( )
,则S21等于( )