题目内容
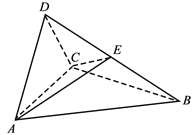
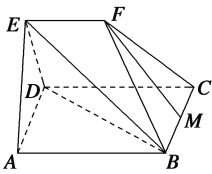
【题目】(12分)如图,已知在直四棱柱![]() 中,
中,
![]() ,
,![]() ,
,![]()
![]() .
.
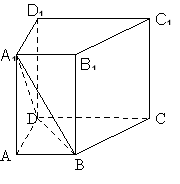
(1)求证:![]() 平面
平面![]() ;
;
(2)设![]() 是
是![]() 上一点,试确定
上一点,试确定![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由.
,并说明理由.
【答案】见解析。
【解析】
试题(1)因为此几何是一个直棱柱,所以![]() .根据线面垂直的判定定理,所以只需再证
.根据线面垂直的判定定理,所以只需再证![]() 即可.
即可.
(2)从图上分析可确定E应为DC的中点,然后证明:四边形A1D1EB是平行四边形,即可得到D1E//A1B,
根据线面平行的判定定理,问题得证.
(1)设![]() 是
是![]() 的中点,连结
的中点,连结![]() ,则四边形
,则四边形![]() 为正方形,
为正方形,
![]() .故
.故![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() .又
.又![]() ,
,![]()
![]() 平面
平面![]() ,
,
(2)证明:DC的中点即为E点,连D1E,BE![]()
![]()
所以四边形ABED是平行四边形所以AD![]() BE,又AD
BE,又AD![]() A1D1
A1D1![]()
![]() A1D1
A1D1
所以四边形A1D1EB是平行四边形 ![]() D1E//A1B ,所以D1E//平面A1BD.
D1E//A1B ,所以D1E//平面A1BD.

练习册系列答案
相关题目
【题目】(13分)编号为A1,A2,…,A16的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | |
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 | |
运动员编号 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | |
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
区间 | [10,20) | [20,30) | [30,40] |
人数 |
(Ⅱ)从得分在区间[20,30)内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50分的概率.