题目内容
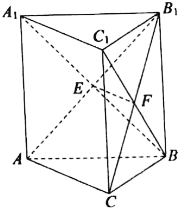
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
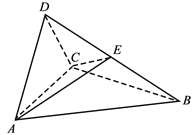
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)利用题意证得二面角的平面角为90°,则可得到面面垂直;
(2)利用题意求得两个半平面的法向量,然后利用二面角的夹角公式可求得二面角D–AE–C的余弦值为![]() .
.
试题解析:(1)由题设可得,![]() ,从而
,从而![]() .
.
又![]() 是直角三角形,所以
是直角三角形,所以![]() .
.
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又由于![]() 是正三角形,故
是正三角形,故![]() .
.
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() .
.
又![]() ,所以
,所以![]() ,
,
故![]() .
.
所以平面ACD⊥平面ABC.
(2)由题设及(1)知,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 为单位长,建立如图所示的空间直角坐标系
为单位长,建立如图所示的空间直角坐标系![]() .则
.则![]() .
.

由题设知,四面体ABCE的体积为四面体ABCD的体积的![]() ,从而E到平面ABC的距离为D到平面ABC的距离的
,从而E到平面ABC的距离为D到平面ABC的距离的![]() ,即E为DB的中点,得
,即E为DB的中点,得![]() .
.
故![]() .
.
设![]() 是平面DAE的法向量,则
是平面DAE的法向量,则 即
即
可取![]() .
.
设![]() 是平面AEC的法向量,则
是平面AEC的法向量,则 同理可取
同理可取![]() .
.
则![]() .
.
所以二面角D-AE-C的余弦值为![]() .
.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】某企业生产了一种新产品,在推广期邀请了100位客户试用该产品,每人一台.试用一个月之后进行回访,由客户先对产品性能作出“满意”或“不满意”的评价,再让客户决定是否购买该试用产品(不购买则可以免费退货,购买则仅需付成本价).经统计,决定退货的客户人数是总人数的一半,“对性能满意”的客户比“对性能不满意”的客户多10人,“对性能不满意”的客户中恰有![]() 选择了退货.
选择了退货.
(1)请完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“客户购买产品与对产品性能满意之间有关”.
的把握认为“客户购买产品与对产品性能满意之间有关”.
对性能满意 | 对性能不满意 | 合计 | |
购买产品 | |||
不购买产品 | |||
合计 |
(2)企业为了改进产品性能,现从“对性能不满意”的客户中按是否购买产品进行分层抽样,随机抽取6位客户进行座谈.座谈后安排了抽奖环节,共有6张奖券,其中一张印有900元字样,两张印有600元字样,三张印有300元字样,抽到奖券可获得相应奖金.6位客户每人随机抽取一张奖券(不放回),设6位客户中购买产品的客户人均所得奖金为![]() 元,求
元,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |