题目内容
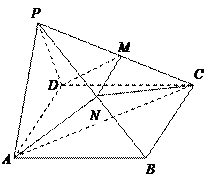
(13分)如图(2):PA⊥面ABCD,CD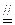 2AB,
2AB,
∠DAB=90°,E为PC的中点.
(1)证明:BE//面PAD;
(2)若PA=AD,证明:BE⊥面PDC.
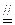 2AB,
2AB, ∠DAB=90°,E为PC的中点.
(1)证明:BE//面PAD;
(2)若PA=AD,证明:BE⊥面PDC.
(1)略 (2)略
(1)取PD的中点M,连ME,MA.
∵E为PC的中点 ∴ME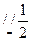 DC,又AB
DC,又AB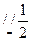 DC ∴ME
DC ∴ME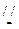 AB.即四边形ABEM为□,∴AM//BE且AM
AB.即四边形ABEM为□,∴AM//BE且AM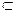 面PAD ∴BE//面PAD.
面PAD ∴BE//面PAD.
(2) ∵PA="AD " ∴AM⊥PD ①
由PA⊥面AC知:PA⊥DC,再由∠DAB=Rt∠,∴DC⊥面PAD ∴DC⊥AM ②
综合①与②知: AM⊥面PDC,由(1)AM//BE 故BE⊥面PDC.
∵E为PC的中点 ∴ME
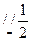 DC,又AB
DC,又AB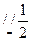 DC ∴ME
DC ∴ME AB.即四边形ABEM为□,∴AM//BE且AM
AB.即四边形ABEM为□,∴AM//BE且AM 面PAD ∴BE//面PAD.
面PAD ∴BE//面PAD.(2) ∵PA="AD " ∴AM⊥PD ①
由PA⊥面AC知:PA⊥DC,再由∠DAB=Rt∠,∴DC⊥面PAD ∴DC⊥AM ②
综合①与②知: AM⊥面PDC,由(1)AM//BE 故BE⊥面PDC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
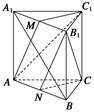
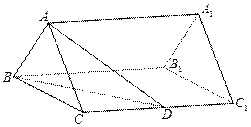 如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.
如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.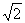 .
.
 a,M是AD的中点。
a,M是AD的中点。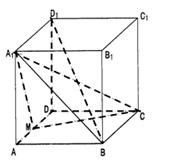
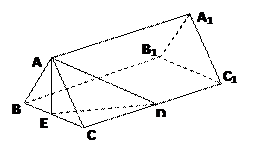 如图,已知正三棱柱
如图,已知正三棱柱 的底面边长是
的底面边长是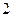 ,
,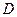 、E是
、E是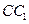 、BC的中点,AE=DE
、BC的中点,AE=DE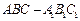 表面积;
表面积; 中,侧面
中,侧面
 垂直,底面
垂直,底面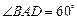 ,
,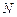 是
是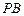 中点,过
中点,过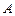 、
、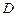 三点的平面交
三点的平面交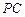 于
于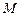 .
. 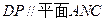 ; (2)求证:
; (2)求证: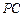 中点;(3)求证:平面
中点;(3)求证:平面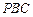 ⊥平面
⊥平面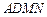 .
. 中,
中, ,则异面直线
,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为



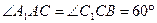 ,且平面ACC1A1⊥平面BCC1B1,则A1B的长度为 。m]
,且平面ACC1A1⊥平面BCC1B1,则A1B的长度为 。m]