题目内容
【挑战自我】
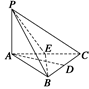
如图,已知PD⊥平面ABCD,AD⊥DC,AD∥BC,PD∶DC∶BC=1∶1∶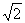 .
.
(1)求二面角D-PB-C的正切值;
(2)当AD∶BC的值是多少时,能使平面PAB⊥平面PBC?证明你的结论.
如图,已知PD⊥平面ABCD,AD⊥DC,AD∥BC,PD∶DC∶BC=1∶1∶
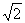 .
.(1)求二面角D-PB-C的正切值;
(2)当AD∶BC的值是多少时,能使平面PAB⊥平面PBC?证明你的结论.

(1)∴二面角D-PB-C的正切值为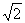
(2)∴当平面PAB⊥平面PBC时,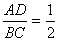
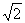
(2)∴当平面PAB⊥平面PBC时,
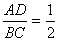
:(1)如图,取PC中点E,连DE.∵PD=DC,∴DE⊥PC.又∵BC⊥DC,BC⊥PD, ∴BC⊥平面PDC,则面BPC⊥面PDC,∴DE⊥面PBC.过E作EF⊥PB于F,连DF,则由三垂线定理有DF⊥PB.∴∠DFE=θ为二面角D-PB-C的平面角.
 设PD=DC=1,则BC=
设PD=DC=1,则BC=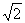 ,DE=
,DE=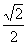 ,PC=
,PC=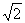 .又∵在Rt△DEF中,tanθ=
.又∵在Rt△DEF中,tanθ=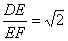
∴二面角D-PB-C的正切值为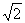
(2)AD∶BC=1∶2时,平面PAB⊥平面PBC.
设PD=1,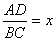 时,平面PAB⊥平面PBC,则DC=1,BC=PC=
时,平面PAB⊥平面PBC,则DC=1,BC=PC=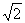 ,AD=
,AD=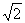 x.
x.
过A作AG⊥PB于G点,∵平面PAB⊥平面PBC,∴AG⊥面PBC,又∵DE⊥面PBC(已证),∴AG∥DE,而AD∥BC,∴AD∥面PBC,故AD∥GE,进而有GE∥BC,又E为PC中点,∴G为PB中点,故GE=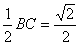 .
.
即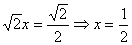 .
.
∴当平面PAB⊥平面PBC时,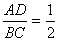
 设PD=DC=1,则BC=
设PD=DC=1,则BC=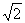 ,DE=
,DE=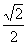 ,PC=
,PC=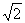 .又∵在Rt△DEF中,tanθ=
.又∵在Rt△DEF中,tanθ=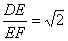
∴二面角D-PB-C的正切值为
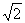
(2)AD∶BC=1∶2时,平面PAB⊥平面PBC.
设PD=1,
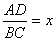 时,平面PAB⊥平面PBC,则DC=1,BC=PC=
时,平面PAB⊥平面PBC,则DC=1,BC=PC=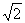 ,AD=
,AD=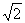 x.
x.过A作AG⊥PB于G点,∵平面PAB⊥平面PBC,∴AG⊥面PBC,又∵DE⊥面PBC(已证),∴AG∥DE,而AD∥BC,∴AD∥面PBC,故AD∥GE,进而有GE∥BC,又E为PC中点,∴G为PB中点,故GE=
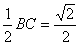 .
.即
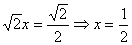 .
.∴当平面PAB⊥平面PBC时,

练习册系列答案
相关题目
 ,
, ,
, 三点都是平面
三点都是平面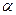 与平面
与平面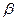 的公共点,并且
的公共点,并且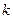 个四面体,则
个四面体,则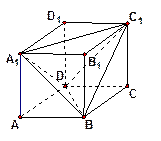
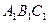 平行于三棱锥
平行于三棱锥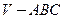 的底面,等边三角形
的底面,等边三角形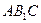 所在平面与面
所在平面与面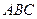 垂直,且
垂直,且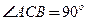 ,设
,设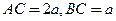 。
。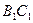 为异面直线
为异面直线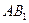 与
与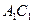 的公垂线;
的公垂线;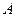 与平面
与平面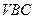 的距离;
的距离;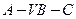 的大小。
的大小。 2AB,
2AB, 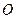 在二面角
在二面角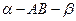 的棱上,点
的棱上,点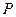 在
在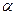 内,且
内,且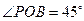 .若对于
.若对于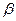 内异于
内异于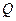 ,都有
,都有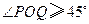 ,则二面角
,则二面角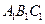 的底面边长均为2,侧棱
的底面边长均为2,侧棱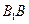 的长为2且与底面ABC所成角为
的长为2且与底面ABC所成角为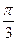 ,且侧面
,且侧面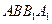 垂直于底面ABC.
垂直于底面ABC.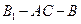 的正切值的大小;
的正切值的大小;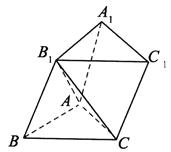 (2)若其余条件不变,只改变侧棱的长度,当侧棱
(2)若其余条件不变,只改变侧棱的长度,当侧棱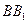 的长度为多长时,可使面
的长度为多长时,可使面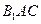 和底面垂直.
和底面垂直. cm
cm )?
)?