题目内容
在数列{an}中,a1=1,当n≥2时,其前n项和Sn满足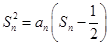 .
.
(1)求Sn的表达式;
(2)设bn=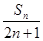 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
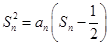 .
.(1)求Sn的表达式;
(2)设bn=
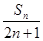 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.(1)因为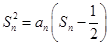 ,所以n≥2,sn2=(sn-sn-1)(sn-
,所以n≥2,sn2=(sn-sn-1)(sn-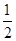 ),
),
所以sn=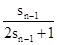 ,即
,即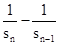 =2(n≥2)
=2(n≥2)
所以,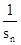 =2n-1
=2n-1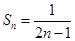 ,
,
(2) 由(1)得,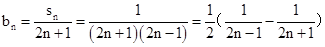
所以,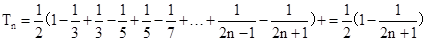 ,
,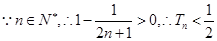
又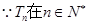 是增函数,
是增函数,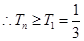 ,故结论得证.
,故结论得证.
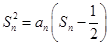 ,所以n≥2,sn2=(sn-sn-1)(sn-
,所以n≥2,sn2=(sn-sn-1)(sn-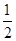 ),
),所以sn=
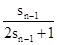 ,即
,即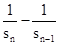 =2(n≥2)
=2(n≥2)所以,
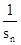 =2n-1
=2n-1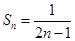 ,
,(2) 由(1)得,
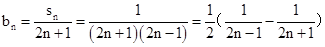
所以,
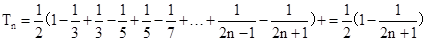 ,
,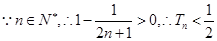
又
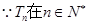 是增函数,
是增函数,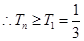 ,故结论得证.
,故结论得证.试题分析:(1)
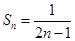 ,(2)
,(2)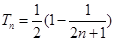
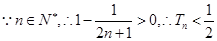
又
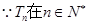 是增函数,
是增函数,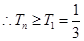 ,故结论得证.
,故结论得证.点评:中档题,本题综合考查数列的前n项和与通项的关系,“裂项相消法”,不等式的证明。涉及
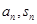 ,往往通过研究
,往往通过研究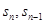 的差,确定数列的通项公式。“裂项相消法”“分组求和法”“错位相减法”是常常考查的数列求和方法。
的差,确定数列的通项公式。“裂项相消法”“分组求和法”“错位相减法”是常常考查的数列求和方法。
练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
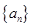 ,
,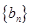 满足
满足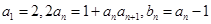 数列
数列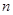 项和为
项和为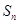 ,
,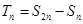 .
.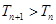 ;
;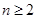 时,
时,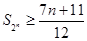 .
.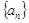 满足
满足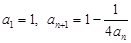 ,其中
,其中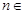 N*.
N*.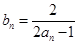 ,求证:数列
,求证:数列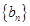 是等差数列,并求出
是等差数列,并求出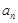 ;
;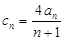 ,数列
,数列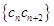 的前
的前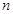 项和为
项和为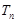 ,是否存在正整数
,是否存在正整数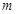 ,使得
,使得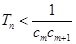 对于
对于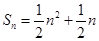
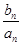 ,求数列
,求数列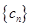 的通项公式
的通项公式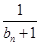 +
+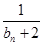 +…+
+…+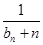 >
>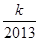 对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.
对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.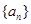 的通项公式
的通项公式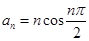 ,其前
,其前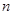 项和为
项和为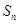 ,则
,则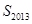 等于( )
等于( )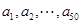 是从-1,0,1这三个整数中取值的数列,若
是从-1,0,1这三个整数中取值的数列,若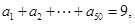
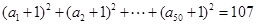 ,则
,则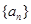 满足:
满足: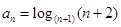 ,定义使
,定义使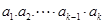 为整数的
为整数的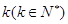 叫做希望数,则区间[1,2013] 内所有希望数的和M=( )
叫做希望数,则区间[1,2013] 内所有希望数的和M=( )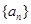 的前
的前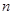 项和为
项和为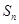 ,且有
,且有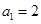 ,
,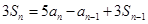
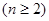 .
.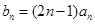 ,求数列
,求数列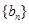 的前
的前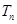 ;
;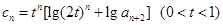 ,且数列
,且数列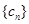 中的 每一项总小于它后面的项,求实数
中的 每一项总小于它后面的项,求实数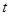 的取值范围.
的取值范围.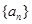 是等比数列,公比
是等比数列,公比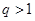 ,前
,前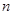 项和为
项和为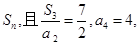
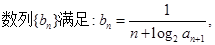
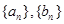 的通项公式;
的通项公式;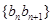 的前
的前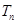 ,求证
,求证