Question

【题目】在正方体ABCD﹣A1B1C1D1中，M和N分别为BC、C1C的中点，那么异面直线MN与AC所成的角等于（ ）
A.30°
B.45°
C.60°
D.90°

Answer 1

【答案】C
【解析】解：如图所示，连接BC1 ． 则MN∥BC1 ． 连接A1C1 ， A1B．
则AC∥A1C1 ，
∴∠BC1A1或其补角是异面直线MN与AC所成的角．
∵△A1BC1是等边三角形．
∴∠A1C1B=60°．
∴异面直线MN与AC所成的角是60°．
故选：C．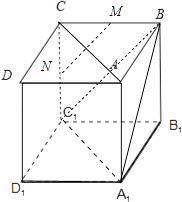

如图所示，连接BC1 ． 则MN∥BC1 ． 连接A1C1 ， A1B．利用正方体的性质可得AC∥A1C1 ， 故∠BC1A1或其补角是异面直线MN与AC所成的角．再利用正方体的性质、等边三角形的性质即可得出．