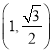题目内容
【题目】若椭圆 
+ 
=1的焦点在x轴上，过点（1， 
）作圆x2+y2=1的切线，切点分别为A，B，直线AB恰好经过椭圆的右焦点和上顶点，则椭圆方程是 ．
【答案】
【解析】解：设过点（1， 
）的圆x2+y2=1的切线为l：y﹣ =k（x﹣1），即kx﹣y﹣k+ =0 ①当直线l与x轴垂直时，k不存在，直线方程为x=1，恰好与圆x2+y2=1相切于点A（1，0）；
②当直线l与x轴不垂直时，原点到直线l的距离为：d= 
=1，解之得k=﹣ 
，
此时直线l的方程为y=﹣ x+ 
，l切圆x2+y2=1相切于点B（ 
， 
）；
因此，直线AB斜率为k1= 
=﹣2，直线AB方程为y=﹣2（x﹣1）
∴直线AB交x轴交于点A（1，0），交y轴于点C（0，2）．
椭圆 
+ 
=1的右焦点为（1，0），上顶点为（0，2）
∴c=1，b=2，可得a2=b2+c2=5，椭圆方程为
所以答案是： ．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
．
练习册系列答案
相关题目
