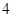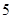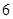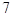题目内容
已知数列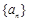 的前n项和
的前n项和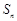 ,满足:
,满足: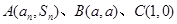 三
三
点共线(a为常数,且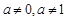 ).
).
(Ⅰ)求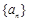 的通项公式;
的通项公式;
(Ⅱ)设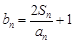 ,若数列
,若数列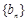 为等比数列,求a的值;
为等比数列,求a的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设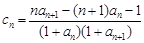 ,数列
,数列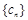 的前n项和为
的前n项和为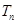 ,是否存在最小的整数m,使得任意的n均有
,是否存在最小的整数m,使得任意的n均有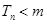 成立?若存在,求出
成立?若存在,求出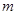 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
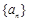 的前n项和
的前n项和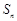 ,满足:
,满足: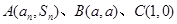 三
三点共线(a为常数,且
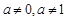 ).
).(Ⅰ)求
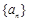 的通项公式;
的通项公式;(Ⅱ)设
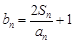 ,若数列
,若数列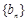 为等比数列,求a的值;
为等比数列,求a的值;(Ⅲ)在满足条件(Ⅱ)的情形下,设
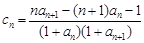 ,数列
,数列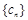 的前n项和为
的前n项和为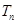 ,是否存在最小的整数m,使得任意的n均有
,是否存在最小的整数m,使得任意的n均有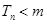 成立?若存在,求出
成立?若存在,求出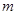 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(Ⅰ) 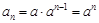 ; (Ⅱ)
; (Ⅱ)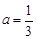 ;(III)
;(III)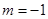 .
.
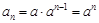 ; (Ⅱ)
; (Ⅱ)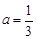 ;(III)
;(III)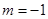 .
.(1)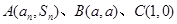 三点共线,则
三点共线,则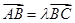 ,
,
(2)在解答题中,当有多个问题时,通常前面问题的结论可为后面的问题提供帮助,如本题中将(1)中的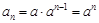 代入(2)
代入(2)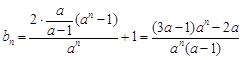 ,即可得
,即可得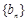 。
。
解:(Ⅰ)由已知可得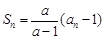
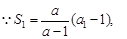 ∴
∴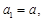
当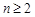 时,
时,
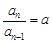 ,即
,即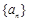 是等比数列. ∴
是等比数列. ∴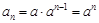 ;
;
(Ⅱ)由(Ⅰ)知,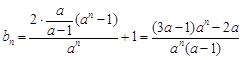 ,
,
若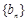 为等比数列,则有
为等比数列,则有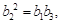
而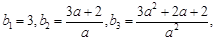
故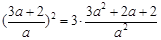 ,解得
,解得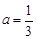 ,
,
再将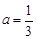 代入得
代入得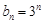 成立,
成立,
所以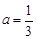 ;
;
(III)证明:由(Ⅱ)知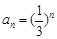 ,
,
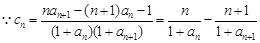
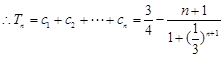
易知 其单调递减,
其单调递减,
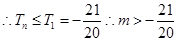 ,
,
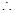 存在最小的整数
存在最小的整数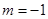 .
.
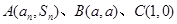 三点共线,则
三点共线,则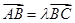 ,
,(2)在解答题中,当有多个问题时,通常前面问题的结论可为后面的问题提供帮助,如本题中将(1)中的
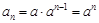 代入(2)
代入(2)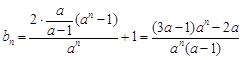 ,即可得
,即可得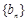 。
。 解:(Ⅰ)由已知可得
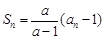
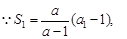 ∴
∴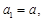
当
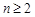 时,
时,
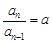 ,即
,即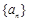 是等比数列. ∴
是等比数列. ∴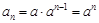 ;
; (Ⅱ)由(Ⅰ)知,
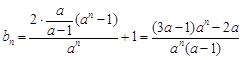 ,
,若
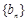 为等比数列,则有
为等比数列,则有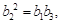
而
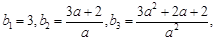
故
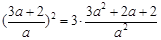 ,解得
,解得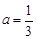 ,
,再将
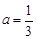 代入得
代入得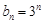 成立,
成立, 所以
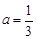 ;
;(III)证明:由(Ⅱ)知
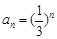 ,
,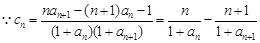
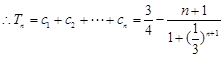
易知
 其单调递减,
其单调递减,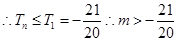 ,
,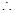 存在最小的整数
存在最小的整数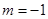 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
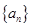 的前
的前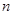 项和为
项和为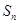 ,已知
,已知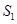 ,
,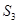 ,
,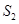 成等差数列.
成等差数列.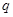 ;
;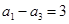 ,求
,求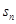 =
=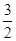
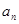 -3,那么这个数列的通项公式是_______.
-3,那么这个数列的通项公式是_______.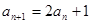 (n=1,2,
(n=1,2, ,
, 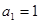 则( )
则( )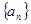 为等比数列
为等比数列 为 等比数列
为 等比数列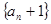 为等比数列
为等比数列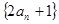 为 等比数列
为 等比数列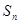 为等比数列
为等比数列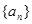 的前
的前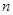 项和,
项和,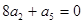 ,则
,则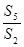 =( )
=( )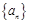 的前
的前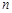 项和为
项和为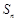 ,若
,若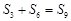 ,则数列
,则数列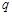 是 .
是 .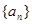 的前
的前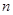 项和为
项和为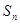 ,对任意
,对任意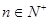 都有
都有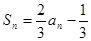 ,若
,若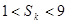
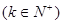 ,则
,则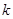 的值为___
的值为___ 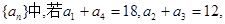 则该数列的前8项之和等于
则该数列的前8项之和等于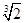 等比数列
等比数列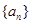 的各项都是正数,且
的各项都是正数,且 ,则( )
,则( )