题目内容
【题目】小明下班回家途经3个有红绿灯的路口,交通法规定:若在路口遇到红灯,需停车等待;若在路口没遇到红灯,则直接通过.经长期观察发现:他在第一个路口遇到红灯的概率为![]() ,在第二、第三个道口遇到红灯的概率依次减小,在三个道口都没遇到红灯的概率为
,在第二、第三个道口遇到红灯的概率依次减小,在三个道口都没遇到红灯的概率为![]() ,在三个道口都遇到红灯的概率为
,在三个道口都遇到红灯的概率为![]() ,且他在各路口是否遇到红灯相互独立.
,且他在各路口是否遇到红灯相互独立.
(1)求小明下班回家途中至少有一个道口遇到红灯的概率;
(2)求小明下班回家途中在第三个道口首次遇到红灯的概率;
(3)记![]() 为小明下班回家途中遇到红灯的路口个数,求数学期望
为小明下班回家途中遇到红灯的路口个数,求数学期望![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据对立事件的概率关系结合已知,即可求解;
(2)设第二、三个道口遇到红灯的概率分别为![]() ,根据已知列出关于
,根据已知列出关于![]() 方程组,求得
方程组,求得![]() ,即可求出结论;
,即可求出结论;
(3)![]() 的可能值为
的可能值为![]() 分别求出概率,得出随机变量的分布列,由期望公式,即可求解.
分别求出概率,得出随机变量的分布列,由期望公式,即可求解.
(1)因为小明在三个道口都没遇到红灯的概率为![]() ,
,
所以小明下班回家途中至少有一个道口遇到红灯的概率为![]() ;
;
(2)设第二、三个道口遇到红灯的概率分别为![]() ,
,
依题意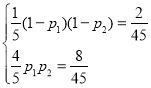 解得
解得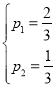 或
或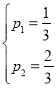 (舍去),
(舍去),
所以小明下班回家途中在第三个道口首次遇到红灯的概率![]() ;
;
(3)![]() 的可能值为
的可能值为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 分布列为
分布列为
|
|
|
|
|
|
|
|
|
|
![]()

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】某周末,郑州方特梦幻王国汇聚了八方来客.面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”,成年人和未成年人选择游玩的意向会有所不同.某统计机构对园区内的100位游客(这些游客只在两个主题公园中二选一)进行了问卷调查.调查结果显示,在被调查的50位成年人中,只有10人选择“西游传说”,而选择“西游传说”的未成年人有20人.
(1)根据题意,请将下面的![]() 列联表填写完整;
列联表填写完整;
选择“西游传说” | 选择“千古蝶恋” | 总计 | |
成年人 | |||
未成年人 | |||
总计 |
(2)根据列联表的数据,判断是否有![]() 的把握认为选择哪个主题公园与年龄有关.
的把握认为选择哪个主题公园与年龄有关.
附参考公式与表: (
(![]() ).
).
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】现从某医院中随机抽取了![]() 位医护人员的关爱患者考核分数(患者考核:
位医护人员的关爱患者考核分数(患者考核:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:
表示;医护专业知识考核分数(试卷考试:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到
的线性回归方程(计算结果精确到![]() );
);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计当某医护人员的医护专业知识考核分数为![]() 分时,他的关爱患者考核分数(精确到
分时,他的关爱患者考核分数(精确到![]() ).
).
参考公式及数据:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
 ,其中
,其中![]() .
.