题目内容
(本小题满分12分)
已知点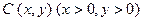 在抛物线
在抛物线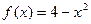 上(如图), 过
上(如图), 过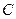 作
作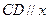 轴交抛物线于另一点
轴交抛物线于另一点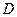 ,设抛物线与
,设抛物线与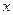 轴相交于
轴相交于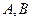 两点,试求
两点,试求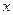 为何值时,梯形
为何值时,梯形 的面积最大,并求出面积的最大值.
的面积最大,并求出面积的最大值.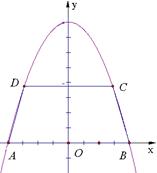
已知点
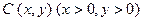 在抛物线
在抛物线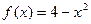 上(如图), 过
上(如图), 过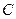 作
作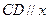 轴交抛物线于另一点
轴交抛物线于另一点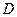 ,设抛物线与
,设抛物线与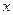 轴相交于
轴相交于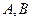 两点,试求
两点,试求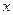 为何值时,梯形
为何值时,梯形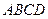 的面积最大,并求出面积的最大值.
的面积最大,并求出面积的最大值.
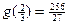
令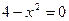 , 得
, 得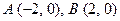 , 又由对称性知
, 又由对称性知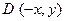 . --- 2分
. --- 2分
设梯形面积为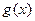 , 则
, 则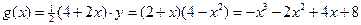 ,
,
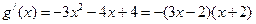 , --- 4分
, --- 4分
令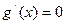 , 因
, 因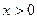 , 得
, 得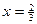 , --- 2分
, --- 2分
当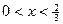 时,
时, 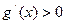 ,
, 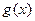 单调递增; 当
单调递增; 当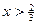 时,
时, 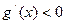 ,
, 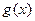 单调递减,
单调递减,
∴ 当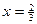 时,
时,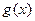 有最大值, 最大值为
有最大值, 最大值为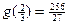 . --- 4分
. --- 4分
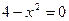 , 得
, 得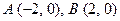 , 又由对称性知
, 又由对称性知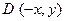 . --- 2分
. --- 2分设梯形面积为
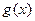 , 则
, 则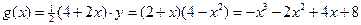 ,
,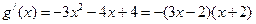 , --- 4分
, --- 4分令
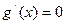 , 因
, 因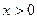 , 得
, 得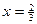 , --- 2分
, --- 2分当
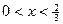 时,
时, 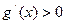 ,
, 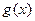 单调递增; 当
单调递增; 当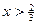 时,
时, 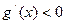 ,
, 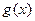 单调递减,
单调递减,∴ 当
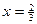 时,
时,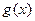 有最大值, 最大值为
有最大值, 最大值为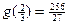 . --- 4分
. --- 4分
练习册系列答案
相关题目
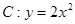 ,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是
,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是 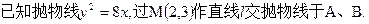
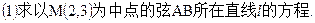
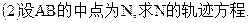
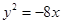 的焦点坐标是
的焦点坐标是 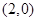
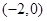
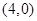
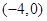
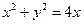 的圆心是抛物线的焦点,直线
的圆心是抛物线的焦点,直线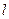 过抛物线的焦点,且斜率为2,直线
过抛物线的焦点,且斜率为2,直线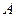 、
、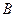 、
、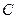 、
、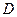 四点.
四点.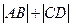 的值.
的值.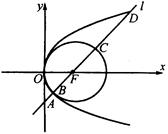
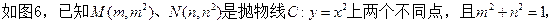
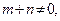 直线
直线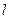 是线段
是线段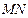 的垂直平分线.设椭圆E的方程为
的垂直平分线.设椭圆E的方程为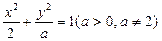 .
.
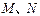 在
在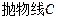 上移动时,求直线
上移动时,求直线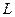 斜率
斜率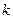 的取值范围;
的取值范围;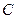 交于A、B两个不同点,
交于A、B两个不同点, 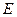 交于P、Q两个不同点,设AB中点为
交于P、Q两个不同点,设AB中点为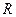 ,OP中点为
,OP中点为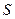 ,若
,若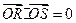 ,求椭圆
,求椭圆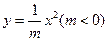 的焦点坐标是
的焦点坐标是  标准方程是 ______
标准方程是 ______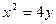 的准线
的准线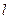 与
与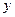 轴交于
轴交于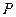 点,若
点,若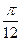 弧度的角速度按逆时针方向旋转,则经过 秒,
弧度的角速度按逆时针方向旋转,则经过 秒,