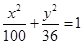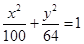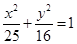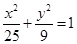题目内容
如图,在平面直角坐标系 中,
中,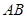 是半圆
是半圆 的直径,
的直径,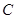 是半圆
是半圆 (除端点
(除端点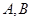 )上的任意一点.在线段
)上的任意一点.在线段 的延长线上取点
的延长线上取点 ,使
,使 ,试求动点
,试求动点 的轨迹方程
的轨迹方程
 中,
中,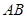 是半圆
是半圆 的直径,
的直径,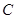 是半圆
是半圆 (除端点
(除端点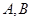 )上的任意一点.在线段
)上的任意一点.在线段 的延长线上取点
的延长线上取点 ,使
,使 ,试求动点
,试求动点 的轨迹方程
的轨迹方程
点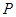 的轨迹方程为
的轨迹方程为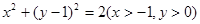
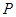 的轨迹方程为
的轨迹方程为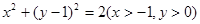
试题分析:[解法一]连结
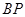 ,由已知可得
,由已知可得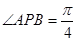 ,
,∴ 点
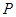 在以
在以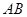 为弦,所对圆周角为
为弦,所对圆周角为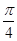 的圆上.
的圆上.设该圆的圆心为
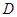 ,则点
,则点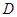 在弦
在弦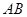 的中垂线上,即
的中垂线上,即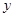 轴上,且
轴上,且 ,
,∴
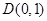 ,
,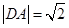 .圆
.圆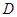 的方程为
的方程为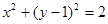 .
.当点
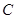 趋近于点
趋近于点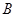 时,点
时,点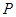 趋近于点
趋近于点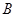 ;当点
;当点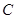 趋近于点
趋近于点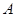 时,点
时,点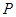 趋近于点
趋近于点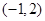 .
.所以点
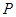 的轨迹方程为
的轨迹方程为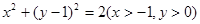
[解法二] 连结
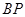 ,由已知可得
,由已知可得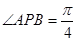 ,
,设
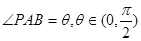 ,则
,则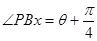
故若设直线
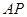 的斜率为
的斜率为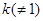 时,直线
时,直线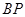 的斜率为
的斜率为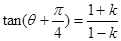 .
.故
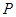 为两直线
为两直线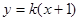 及
及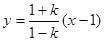 的交点,消去
的交点,消去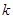 得
得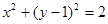 ,当
,当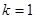 时,
时,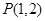 也在该圆上.
也在该圆上.结合
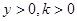 可知,点
可知,点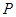 的轨迹方程为
的轨迹方程为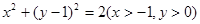
点评:解决该试题的关键是建立动点满足的关系式,设出点的坐标,建立关系式,将关系式坐标化,然后化简得到其轨迹方程,一般来说,先考虑运用定义法求解轨迹,再考虑运用直接法来求解,中档题。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
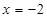 ,则抛物线方程是( )
,则抛物线方程是( )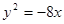 ,
,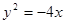
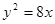
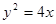
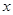 在轴上,离心率
在轴上,离心率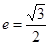 ,已知点
,已知点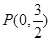 到这个椭圆上的最远距离是
到这个椭圆上的最远距离是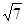 ,求这个椭圆的方程.
,求这个椭圆的方程.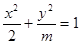 的焦点在
的焦点在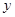 轴上,离心率为
轴上,离心率为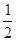 ,则
,则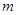 的值为( )
的值为( )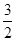
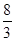
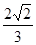
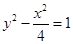 的两条渐近线和抛物线y2 ="-8x" 的准线所围成的三角形(含边界与内部).若点(x,y) ∈ D,则x+ y的最小值为
的两条渐近线和抛物线y2 ="-8x" 的准线所围成的三角形(含边界与内部).若点(x,y) ∈ D,则x+ y的最小值为 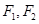 是双曲线
是双曲线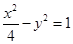 的两个焦点,
的两个焦点, 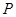 在双曲线上且
在双曲线上且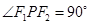 ,则
,则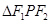 的面积为 ( )
的面积为 ( )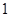
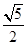
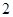
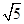
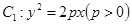 的焦点
的焦点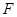 恰好是曲线
恰好是曲线 的右焦点,且曲线
的右焦点,且曲线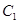 与曲线
与曲线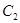 交点连线过点
交点连线过点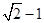
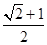
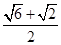
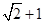
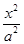 +
+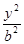 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是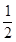 ,则
,则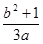 的最小值为( )
的最小值为( )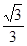
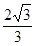
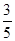 ,则此椭圆的方程是
,则此椭圆的方程是