题目内容
【题目】已知![]() ,函数
,函数![]() (
(![]() 是自然对数的底数).
是自然对数的底数).
(Ⅰ)若![]() ,证明:曲线
,证明:曲线![]() 没有经过点
没有经过点![]() 的切线;
的切线;
(Ⅱ)若函数![]() 在其定义域上不单调,求
在其定义域上不单调,求![]() 的取值范围;
的取值范围;
(Ⅲ)是否存在正整数![]() ,当
,当![]() 时,函数
时,函数![]() 的图象在
的图象在![]() 轴的上方,若存在,求
轴的上方,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() ;(Ⅲ)答案见解析.
;(Ⅲ)答案见解析.
【解析】试题分析:(Ⅰ)求出函数的导数,求出切线方程,化简得: ![]() ,令
,令![]() ,根据函数的单调性判断方程
,根据函数的单调性判断方程![]() 无解,从而证明结论即可;(Ⅱ)分离参数,得
无解,从而证明结论即可;(Ⅱ)分离参数,得![]() ,令
,令![]() (
(![]() ),根据函数的单调性求出参数的范围即可;(Ⅲ)问题等价于
),根据函数的单调性求出参数的范围即可;(Ⅲ)问题等价于![]() ,令
,令![]() ,根据函数的单调性求出
,根据函数的单调性求出![]() 的最小值,从而证明结论即可;
的最小值,从而证明结论即可;
试题解析:(Ⅰ)因为![]() ,所以
,所以![]() ,此时
,此时![]() ,
,
设曲线![]() 在点
在点![]() 处的切线经过点
处的切线经过点![]()
则曲线![]() 在点
在点![]() 处的切线
处的切线![]()
所以![]()
化简得: ![]()
令![]() ,则
,则![]() ,
,
所以当![]() 时,
时, ![]() ,
, ![]() 为减函数,
为减函数,
当![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数,
所以![]() ,
,
所以![]() 无解
无解
所以曲线![]() 的切线都不经过点
的切线都不经过点![]()
(Ⅱ)函数的定义域为![]() ,因为
,因为![]() ,
,
所以![]() 在定义域上不单调,等价于
在定义域上不单调,等价于![]() 有变号零点,
有变号零点,
令![]() ,得
,得![]() ,令
,令![]() (
(![]() ).
).
因为![]() ,令
,令![]() ,
, ![]() ,
,
所以![]() 是
是![]() 上的减函数,又
上的减函数,又![]() ,故
,故![]() 是
是![]() 的唯一零点,
的唯一零点,
当![]() ,
, ![]() ,
, ![]() ,
, ![]() 递增;
递增;
当![]() ,
, ![]() ,
, ![]() ,
, ![]() 递减;
递减;
故当![]() 时,
时, ![]() 取得极大值且为最大值
取得极大值且为最大值![]() ,
,
所以![]() ,即
,即![]() 的取值范围是
的取值范围是![]()
(Ⅲ)函数![]() 的图象在
的图象在![]() 轴的上方,即对任意
轴的上方,即对任意![]() ,
, ![]() 恒成立.
恒成立.
![]()
![]() .令
.令![]() (
(![]() ),
),
所以![]()
(1)当![]() 时,
时, ![]() ,即
,即![]()
①当![]() 时,
时, ![]() ,
, ![]() 是减函数,所以
是减函数,所以![]() ;
;
②当![]() 时,
时, 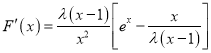 ,
,
令![]() ,则
,则![]() ,所以
,所以![]() 是增函数,
是增函数,
所以当![]() 时,
时, ![]() ,即
,即![]()
所以![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,
,
当![]() 时,取
时,取![]() ,且使
,且使![]() ,即
,即![]() ,
,
则![]() ,
,
因为![]() ,故
,故![]() 存在唯一零点
存在唯一零点![]() ,
,
即![]() 有唯一的极值点且为最小值点
有唯一的极值点且为最小值点![]()
所以![]() ,又
,又![]() ,即
,即![]() ,
,
故![]() ,设
,设![]() ,
,
因为![]() ,所以
,所以![]() 是
是![]() 上的减函数,
上的减函数,
所以![]() ,即
,即![]()
所以当![]() 时,对任意
时,对任意![]() ,
, ![]() 恒成立
恒成立
(2)当![]() 时,
时, ![]() ,因为
,因为![]() ,取
,取![]() ,
,
则![]() ,
, ![]() ,
,
所以![]() 不恒成立,
不恒成立,
综上所述,存在正整数![]() 满足要求,即当
满足要求,即当![]() 时,函数
时,函数![]() 的图象在
的图象在![]() 轴的上方
轴的上方

【题目】某同学用“五点法”画函数f(x)=Asin(ωx+![]() )(A>0,ω>0,|
)(A>0,ω>0,|![]() |<
|<![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+ | 0 | 5 | -5 | 0 |
(1)请将上表数据补充完整,并求出函数f(x)的解析式;
(2)将y=f(x)的图象向左平移![]() 个单位,得到函数y=g(x)的图象.若关于x的方程g(x)-m=0在区间[0,
个单位,得到函数y=g(x)的图象.若关于x的方程g(x)-m=0在区间[0,![]() ]上有两个不同的解,求实数m的取值范围.
]上有两个不同的解,求实数m的取值范围.




