题目内容
【题目】已知椭圆![]() ,如图所示点
,如图所示点![]() 为椭圆上任意三点.
为椭圆上任意三点.

(Ⅰ)若![]() ,是否存在实数
,是否存在实数![]() ,使得代数式
,使得代数式![]() 为定值.若存在,求出实数
为定值.若存在,求出实数![]() 和
和![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅱ)若![]() ,求三角形
,求三角形![]() 面积的最大值;
面积的最大值;
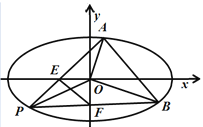
(Ⅲ)满足(Ⅱ),且在三角形![]() 面积取得最大值的前提下,若线段
面积取得最大值的前提下,若线段![]() 与椭圆长轴和短轴交于点
与椭圆长轴和短轴交于点![]() (
(![]() 不是椭圆的顶点).判断四边形
不是椭圆的顶点).判断四边形![]() 的面积是否为定值.若是,求出定值;若不是,说明理由.
的面积是否为定值.若是,求出定值;若不是,说明理由.
【答案】(1)![]() ,
,![]() (2)1(3)2
(2)1(3)2
【解析】试题分析:(1)将坐标代入椭圆方程,根据![]() ,消去
,消去![]() 得
得![]() (2)由
(2)由![]() ,得
,得![]() 联立直线方程与椭圆方程,利用韦达定理以及弦长公式求AB,根据点到直线距离公式求三角形高,再代入三角形面积公式,最后根据基本不等式求最值,(3)先求E,F坐标,再根据四边形面积公式求面积,计算结果为定值即可.
联立直线方程与椭圆方程,利用韦达定理以及弦长公式求AB,根据点到直线距离公式求三角形高,再代入三角形面积公式,最后根据基本不等式求最值,(3)先求E,F坐标,再根据四边形面积公式求面积,计算结果为定值即可.
试题解析:(Ⅰ)由于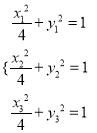 ,且
,且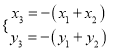 ;
;
得: 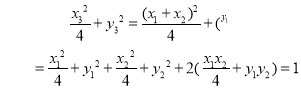
所以![]() ,即
,即![]()
故,存在实数![]() 使得
使得![]() .
.
(Ⅱ)当直线![]() 斜率不存在时,可设为
斜率不存在时,可设为![]() ;
;
联立方程组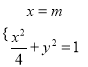 ,得
,得![]() ;
;
由![]() ,得
,得![]() ,即
,即![]() ,
, ![]() ;
;
当直线![]() 斜率存在时,可设为
斜率存在时,可设为![]() ;
;
联立方程组 ,得
,得![]() ;
;
![]()
由![]() ,得
,得![]() ,
,
即![]() ,
, ![]()
![]() ,
, ![]() ;
;
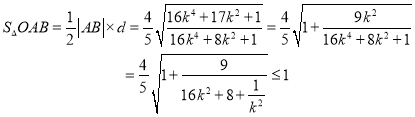
等号成立时, ![]() ,即
,即![]() .
.
所以![]() 的最大值为1.
的最大值为1.
(Ⅲ)![]() 取得最大值时,
取得最大值时, ![]() ,此时直线
,此时直线![]() 与坐标轴的交点恰好分别是椭圆长轴和短轴各一个端点;
与坐标轴的交点恰好分别是椭圆长轴和短轴各一个端点;
不妨取![]() ,
, ![]() ,若线段
,若线段![]() 与椭圆长轴和短轴交于点
与椭圆长轴和短轴交于点![]() (
(![]() 不是椭圆与坐标轴的交点).
不是椭圆与坐标轴的交点).
此时点![]() 定在第三象限,即
定在第三象限,即![]() ;
;
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]()
同理,得![]()
四边形![]() 的面积为:
的面积为:
![]()

【题目】为了了解某省各景点在大众中的熟知度,随机对15~65岁的人群抽样了![]() 人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组 | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
【题目】某市A,B,C,D四所中学报名参加某高校2015年自主招生考试的学生人数如下表所示:
中学 | A | B | C | D |
人数 | 40 | 30 | 10 | 20 |
该市教委为了解参加考试的学生的学习状况,采用分层抽样的方法从四所中学报名参加考试的学生中随机抽取50名参加问卷调查.则A,B,C,D四所中学抽取的学生人数分别为( )
A.15,20,10,5B.15,20,5,10
C.20,15,10,5D.20,15,5,10
【题目】治理大气污染刻不容缓,根据我国分布的《环境空气质量数(AQI)技术规定》:空气质量指数划分阶为0~50、51~100、101~150、151~200、201~300和大于300六级,对应于空气质量指数的六个级别,指数越大,级别越高,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数小于![]() 时,可以户外运动;空气质量指数
时,可以户外运动;空气质量指数![]() 及以上,不适合进行旅游等户外活动,以下是某市
及以上,不适合进行旅游等户外活动,以下是某市![]() 年
年![]() 月中旬的空气质量指数情况:
月中旬的空气质量指数情况:
时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
AQI | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
(1)求![]() 月中旬市民不适合进行户外活动的概率;
月中旬市民不适合进行户外活动的概率;
(2)一外地游客在![]() 月中旬来该市旅游,想连续游玩两天,求适合旅游的概率.
月中旬来该市旅游,想连续游玩两天,求适合旅游的概率.


