题目内容
(1)已知f(x)=sinx+2sin( +
+ )cos(
)cos( +
+ ).(1)若f(α)=
).(1)若f(α)= ,α∈(-
,α∈(- ,0),求α的值;
,0),求α的值;
(2)若sin =
= ,x∈(
,x∈( ,π),求f(x)的值.
,π),求f(x)的值.
(1)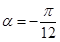 ;(2)
;(2)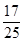 .
.
解析试题分析:(1)首先根据三角函数公式对函数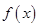 进行化简,即
进行化简,即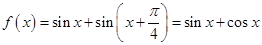 ,从而
,从而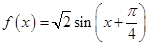 ,则
,则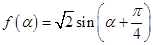 ,再由
,再由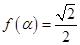 ,又
,又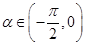 ,从而求出
,从而求出 的值.(2)由
的值.(2)由 ,则
,则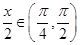 ,根据同角平方关系,由
,根据同角平方关系,由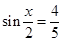 ,得
,得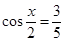 ,再由倍角公式,可得
,再由倍角公式,可得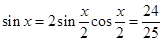 ,
,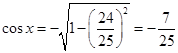 ,从而求出函数
,从而求出函数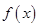 的值.
的值.
试题解析:(1)f(x)=sin x+2sin( +
+ )cos(
)cos( +
+ )
)
=sin x+sin(x+ )=sin x+cos x=
)=sin x+cos x=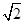 sin(x+
sin(x+ ),
),
由f(α)= ,得
,得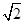 sin(α+
sin(α+ )=
)= .
.
∴sin(α+ )=
)=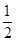 .
.
∵α∈(- ,0),∴α+
,0),∴α+ ∈(-
∈(- ,
, ).
).
∴α+ =
=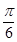 .∴α=-
.∴α=-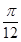 .
.
(2)∵x∈( ,π),∴
,π),∴ ∈(
∈( ,
, ).
).
又sin =
= ,∴cos
,∴cos =
=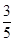 .
.
∴sin x=2sin cos
cos =
=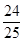 ,
,
cos x=-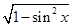 =-
=-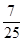 .
.
∴f(x)=sin x+cos x=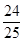 -
-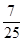 =
=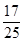 .
.
考点:三角函数的公式及化简求值.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,钝角
,钝角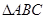 (角
(角 对边为
对边为 )的角
)的角 满足
满足 .
. 的单调递增区间;
的单调递增区间; ,求
,求 .
. 中,已知
中,已知 .
. ;
;  求角A的大小.
求角A的大小. .
. 的单调减区间;
的单调减区间; 上最大值和最小值.
上最大值和最小值. (
( )的最小正周期为
)的最小正周期为 .求函数
.求函数 的单调增区间;
的单调增区间; 中,角
中,角 对边分别是
对边分别是 ,且满足
,且满足 .若
.若 ,
, .求角
.求角 的大小和边b的长.
的大小和边b的长.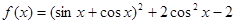 .
. 的最小正周期;
的最小正周期;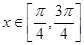 时,求函数
时,求函数

 ,函数
,函数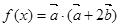 .
. 的单调递增区间;
的单调递增区间; 成立的
成立的 的取值集合.
的取值集合. 与
与 ,其中
,其中
 ,求
,求 和
和 的值;
的值; ,求
,求 的值域.
的值域. .
. 的最小正周期;
的最小正周期; 上的函数值的取值范围.
上的函数值的取值范围.