题目内容
已知数列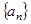 的各项均是正数,其前
的各项均是正数,其前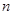 项和为
项和为 ,满足
,满足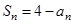 .
.
(I)求数列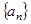 的通项公式;
的通项公式;
(II)设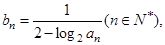 数列
数列 的前
的前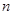 项和为
项和为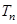 ,求证:
,求证: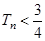 .
.
(Ⅰ)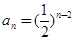 . (Ⅱ)详见解析.
. (Ⅱ)详见解析.
解析试题分析:(Ⅰ)首先令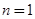 求出首项
求出首项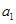 ,
,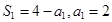 .
.
由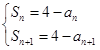 两式相减,得
两式相减,得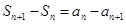 即
即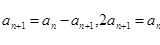 .所以
.所以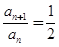 ,
,
数列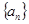 是首项为2,公比为
是首项为2,公比为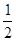 的等比数列.由等比数列的通项公式便可得数列
的等比数列.由等比数列的通项公式便可得数列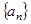 的通项公式.
的通项公式.
(Ⅱ)证明有关数列前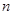 项和的不等式,一般有以下两种思路:一种是先求和后放缩,一种是先放缩后求和.在本题中,由(Ⅰ)可得:
项和的不等式,一般有以下两种思路:一种是先求和后放缩,一种是先放缩后求和.在本题中,由(Ⅰ)可得: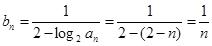 ,
,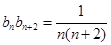 .这显然用裂项法求和,然后用放缩法即可证明.
.这显然用裂项法求和,然后用放缩法即可证明.
试题解析:(Ⅰ)由题设知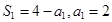 , 2分
, 2分
由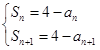 两式相减,得
两式相减,得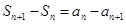 .
.
所以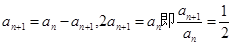 . 4分
. 4分
可见,数列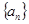 是首项为2,公比为
是首项为2,公比为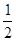 的等比数列。
的等比数列。
所以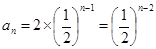 6分
6分
(Ⅱ)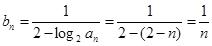 , 8分
, 8分 . 10分
. 10分
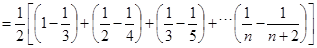
=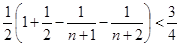 . 12分
. 12分
考点:1、等比数列;2、裂项法;3、不等式的证明.

练习册系列答案
相关题目
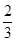 an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数. ,求数列
,求数列 的前n项和.
的前n项和. 元,第n+l个月月底余
元,第n+l个月月底余 元,写出a1的值并建立
元,写出a1的值并建立
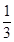 )是函数
)是函数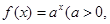 且
且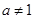 )的图象上一点,等比数列
)的图象上一点,等比数列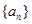 的前
的前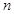 项和为
项和为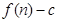 ,数列
,数列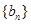
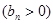 的首项为
的首项为 ,且前
,且前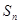 满足
满足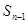 =
=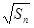 +
+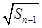 (
(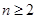 ).
).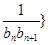 前
前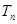 ,问
,问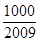 的最小正整数
的最小正整数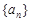 满足
满足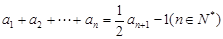 .
. 与
与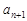 之间插入
之间插入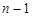 个数连同
个数连同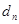 (
(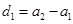 )的等差数列.
)的等差数列.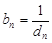 ,求数列
,求数列 的前
的前 和
和 ;
;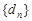 中是否存在三项
中是否存在三项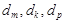 (其中
(其中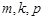 成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.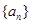 满足
满足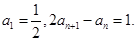
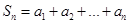
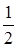 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n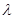 ·bn+1(
·bn+1(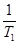 +
+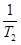 +
+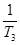 + +
+ +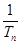 与
与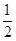 Sn的大小.
Sn的大小. 的前n项和
的前n项和 ,且
,且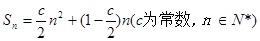 ,且
,且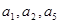 成公比不等于1的等比数列。
成公比不等于1的等比数列。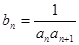 ,求数列{
,求数列{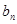 }的前n项和Tn.
}的前n项和Tn.