题目内容
【题目】在平面直角坐标系xOy中,已知椭圆 ![]() =l (a>b>0)的焦距为2,离心率为
=l (a>b>0)的焦距为2,离心率为 ![]() ,椭圆的右顶点为A.
,椭圆的右顶点为A.
(1)求该椭圆的方程:
(2)过点D( ![]() ,﹣
,﹣ ![]() )作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
)作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
斜率之和为定值.
【答案】
(1)
解:由题意可知:椭圆 ![]() =l (a>b>0),焦点在x轴上,2c=1,c=1,
=l (a>b>0),焦点在x轴上,2c=1,c=1,
椭圆的离心率e= ![]() =
= ![]() ,则a=
,则a= ![]() ,b2=a2﹣c2=1,
,b2=a2﹣c2=1,
则椭圆的标准方程: ![]()
(2)
解:证明:设P(x1,y1),Q(x2,y2),A( ![]() ,0),
,0),
由题意PQ的方程:y=k(x﹣ ![]() )﹣
)﹣ ![]() ,
,
则 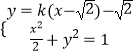 ,整理得:(2k2+1)x2﹣(4
,整理得:(2k2+1)x2﹣(4 ![]() k2+4
k2+4 ![]() k)x+4k2+8k+2=0,
k)x+4k2+8k+2=0,
由韦达定理可知:x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
则y1+y2=k(x1+x2)﹣2 ![]() k﹣2
k﹣2 ![]() =
= ![]() ,
,
则kAP+kAQ= ![]() +
+ ![]() =
= ![]() ,
,
由y1x2+y2x1=[k(x1﹣ ![]() )﹣
)﹣ ![]() ]x2+[k(x2﹣
]x2+[k(x2﹣ ![]() )﹣
)﹣ ![]() ]x1=2kx1x2﹣(
]x1=2kx1x2﹣( ![]() k+
k+ ![]() )(x1+x2)=﹣
)(x1+x2)=﹣ ![]() ,
,
kAP+kAQ= ![]() =
= 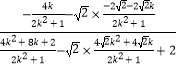 =1,
=1,
∴直线AP,AQ的斜率之和为定值1
【解析】(1)由题意可知2c=2,c=1,离心率e= ![]() ,求得a=2,则b2=a2﹣c2=1,即可求得椭圆的方程:(2)则直线PQ的方程:y=k(x﹣
,求得a=2,则b2=a2﹣c2=1,即可求得椭圆的方程:(2)则直线PQ的方程:y=k(x﹣ ![]() )﹣
)﹣ ![]() ,代入椭圆方程,由韦达定理及直线的斜率公式,分别求得直线AP,AQ的斜率,即可证明直线AP,AQ的率之和为定值.
,代入椭圆方程,由韦达定理及直线的斜率公式,分别求得直线AP,AQ的斜率,即可证明直线AP,AQ的率之和为定值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目