题目内容
19.设α∈(0,$\frac{π}{2}$),β∈[0,$\frac{π}{2}$],则2α-$\frac{β}{3}$的取值范围是$(-\frac{π}{6},π)$.分析 利用不等式的基本性质即可得出.
解答 解:∵α∈(0,$\frac{π}{2}$),β∈[0,$\frac{π}{2}$],
∴2α∈(0,π),$-\frac{β}{3}$∈$[-\frac{π}{6},0]$.
∴2α-$\frac{β}{3}$∈$(-\frac{π}{6},π)$.
则2α-$\frac{β}{3}$的取值范围是$(-\frac{π}{6},π)$.
故答案为:$(-\frac{π}{6},π)$.
点评 本题考查了不等式的基本性质,属于基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
10.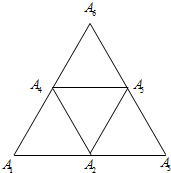 如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )
如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )
 如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )
如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )| A. | {-2,-1,0,1,2} | B. | $\left\{{-2,-1,-\frac{1}{2},0,\frac{1}{2},1,2}\right\}$ | ||
| C. | $\left\{{-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2}}\right\}$ | D. | $\left\{{-2,-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2},2}\right\}$ |
15.如图是一算法的程序框图,若此程序运行结果为s=55,则在判断框中应填入关于k的判断条件是( )


| A. | k≤11 | B. | k≤10 | C. | k≤9 | D. | k≤8 |
 如图所示的圆内接四边形ABCD中,∠ABC>$\frac{π}{2}$,∠ADB=∠CDB,DB交AC于点E.若△ADC的面积S=$\frac{\sqrt{3}}{4}$DE•DB,则∠ADC的大小为$\frac{π}{3}$.
如图所示的圆内接四边形ABCD中,∠ABC>$\frac{π}{2}$,∠ADB=∠CDB,DB交AC于点E.若△ADC的面积S=$\frac{\sqrt{3}}{4}$DE•DB,则∠ADC的大小为$\frac{π}{3}$.