题目内容
(本小题满分12分)已知函数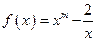 ,且
,且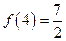 。
。
(1)求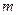 的值;
的值;
(2)判定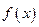 的奇偶性;
的奇偶性;
(3)判断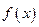 在
在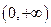 上的单调性,并给予证明。
上的单调性,并给予证明。
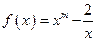 ,且
,且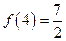 。
。(1)求
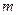 的值;
的值;(2)判定
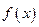 的奇偶性;
的奇偶性;(3)判断
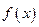 在
在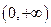 上的单调性,并给予证明。
上的单调性,并给予证明。
略

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
题目内容
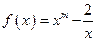 ,且
,且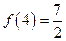 。
。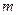 的值;
的值;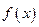 的奇偶性;
的奇偶性;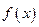 在
在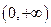 上的单调性,并给予证明。
上的单调性,并给予证明。

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案