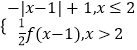题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,数列
,数列![]() 的通项公式为
的通项公式为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
①求![]() ;
;
②若![]() ,求数列
,求数列![]() 的最小项的值.
的最小项的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)由![]() 与
与![]() 的关系得
的关系得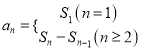 ,又
,又![]() ,
,
![]() ;(2)由(1)得
;(2)由(1)得![]() ,讨论
,讨论![]() 分别用公式法和错误相减法求和;
分别用公式法和错误相减法求和;
![]() 时,
时, ![]() =
=![]() ,构造函数研究单调性得最小值
,构造函数研究单调性得最小值
(1)an=![]() =2n.…………………4分
=2n.…………………4分
(若没有交待a1扣1分)
(2)cn=![]() .
.
Tn=2+4x+6x2+8x3+……+![]() . ①
. ①
则xTn=2x+4x2+6x3+8x3+……+![]() . ②
. ②
①-②,得(1-x)Tn=2+2x+2x2+……+![]() -
-![]() .
.
当x≠1时,(1-x)Tn=2×![]() -
-![]() .所以Tn=
.所以Tn=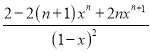 .…8分
.…8分
当x=1时,Tn=2+4+6+8+……+2n=n2+n.…………………10分
(3)当x=2时,Tn=2+![]() .
.
则![]() =
=![]() . ……………………11分
. ……………………11分
设f(n)=![]() .
.
因为f(n+1)-f(n)=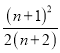 -
-![]() =
=![]() >0, …………14分
>0, …………14分
所以函数f(n)在n∈N+上是单调增函数. …………………15分
所以n=1时,f(n)取最小值![]() ,即数列{
,即数列{![]() }的最小项的值为
}的最小项的值为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目