题目内容
【题目】如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE且CE=AC=2BD,试在AE上确定一点M,使得DM∥平面ABC. 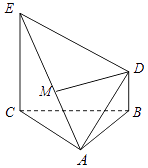
【答案】解:取AE中点为M,取AC中点为N,连结MD,MN,NB,
在△ABC中,∵M,N分别是边AC,AE的中点,∴CE=2MN且MN∥CE,
又∵CE=2BD且BD∥CE,
∴MN∥BD且MN=BD,
∴四边形BDMN是平行四边形.
∴DM∥BN,
又∵BN平面ABC,DM平面ABC,
∴DM∥平面ABC.
故M为AE的中点时,DM∥平面ABC.
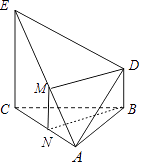
【解析】AE中点为M,取AC中点为N,通过证明四边形MNBD是平行四边形得出DM∥BN,从而可得DM∥平面ABC.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

练习册系列答案
相关题目