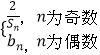题目内容
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() 、
、 ![]() ,短轴两个端点为
,短轴两个端点为 ![]() 、
、 ![]() ,且四边形
,且四边形 ![]() 是边长为2的正方形.
是边长为2的正方形.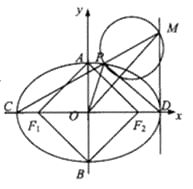
(1)求椭圆的方程;
(2)若 ![]() 、
、 ![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 ![]() 满足
满足 ![]() ,连接
,连接 ![]() ,交椭圆于点
,交椭圆于点 ![]() .证明:
.证明: ![]() 为定值.
为定值.
(3)在(2)的条件下,试问 ![]() 轴上是否存异于点
轴上是否存异于点 ![]() 的定点
的定点 ![]() ,使得以
,使得以 ![]() 为直径的圆恒过直线
为直径的圆恒过直线 ![]() 、
、 ![]() 的交点,若存在,求出点
的交点,若存在,求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】
(1)解: ![]() ,∴
,∴ ![]() 椭圆方程为:
椭圆方程为: ![]() .
.
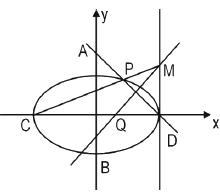
(2)解:∵ ![]() ,∴设
,∴设 ![]() ,则直线
,则直线 ![]() 的方程为:
的方程为: ![]() ,
,
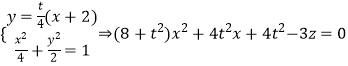 ,
,
解设: ![]() 或
或 ![]() (舍去),
(舍去),
![]() ,∴
,∴ ![]() ,从而
,从而 ![]() ,
,
∴ ![]()
(3)解:设 ![]() ,若以
,若以 ![]() 为直径的圆过
为直径的圆过 ![]() 与
与 ![]() 的交点即直线
的交点即直线 ![]() ,
,
直线 ![]() 的斜率
的斜率 ![]() ,直线
,直线 ![]() 的斜率
的斜率 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,
,
∴ ![]() ,即
,即 ![]()
【解析】(1)根据题意结合椭圆中a2=b2+c2的关系分别求出a、b的值进而求出椭圆的方程。(2)由已知利用点斜式设出直线MC的方程,联立椭圆和直线的方程消去y得到的关于x的方程,解出点P和点M的坐标由向量的数量积的坐标表示计算即可得到定值为4。(3)根据题意设出点Q的坐标,利用直径所对的圆心角为直角得出垂直的关系,再转化为向量的数量积等于零,即可解得Q点的坐标。
【考点精析】掌握椭圆的概念是解答本题的根本,需要知道平面内与两个定点![]() ,
,![]() 的距离之和等于常数(大于
的距离之和等于常数(大于![]() )的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.
)的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】已知二次函数![]() 的最小值为3,且
的最小值为3,且![]() .
.
求函数![]() 的解析式;
的解析式;
(2)若偶函数![]() (其中
(其中![]() ),那么,
),那么, ![]() 在区间
在区间![]() 上是否存在零点?请说明理由.
上是否存在零点?请说明理由.
【答案】(1)![]() (2)存在零点
(2)存在零点
【解析】试题分析:(1)待定系数法,己知函数类型为二次函数,又知f(-1)=f(3),所以对称轴是x=1,且函数最小值f(1)=3,所设函数![]() ,且
,且![]() ,代入f(-1)=11,可解a。
,代入f(-1)=11,可解a。
(2)由题意可得![]() ,代入
,代入![]() ,由
,由![]() 和根的存在性定理,
和根的存在性定理, ![]() 在区间(1,2)上存在零点。
在区间(1,2)上存在零点。
试题解析:(1)因为![]() 是二次函数,且
是二次函数,且![]()
所以二次函数图像的对称轴为![]() .
.
又![]() 的最小值为3,所以可设
的最小值为3,所以可设![]() ,且
,且![]()
由![]() ,得
,得![]()
所以![]()
(2)由(1)可得![]() ,
,
因为![]() ,
,
![]()
所以![]() 在区间(1,2)上存在零点.
在区间(1,2)上存在零点.
【点睛】
(1)对于求己知类型函数的的解析式,常用待定系数法,由于二次函数的表达式形式比较多,有一般式,两点式,顶点式,由本题所给条件知道对称轴与顶点坐标,所以设顶点式。
(2)对于判定函数在否存在零点问题,一般解决此类问题的三步曲是:①先通过观察函数图象再估算出根所在的区间;②根据方程根的存在性定理证明根是存在的;③最后根据函数的性质证明根是唯一的.本题给了区间,可直接用根的存在性定理。
【题型】解答题
【结束】
20
【题目】《中华人民共和国个人所得税》规定,公民月工资、薪金所得不超过3500元的部分不纳税,超过3500元的部分为全月税所得额,此项税款按下表分段累计计算:
全月应纳税所得额 | 税率 |
不超过1500元的部分 |
|
超过1500元至4500元的部分 |
|
超过4500元至9000元的部分 |
|
(1)已知张先生的月工资,薪金所得为10000元,问他当月应缴纳多少个人所得税?
(2)设王先生的月工资,薪金所得为![]() ,当月应缴纳个人所得税为
,当月应缴纳个人所得税为![]() 元,写出
元,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)已知王先生一月份应缴纳个人所得税为303元,那么他当月的工资、薪金所得为多少?
【题目】某港口水的深度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t).下面是某日水深的数据:
t/h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y/m | 10 | 13 | 10 | 7 | 10 | 13 | 10 | 7 | 10 |
经长期观察,y=f(t)的曲线可以近似地看成函数![]() 的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
(1)求y与t满足的函数关系式;
(2)某船吃水深度(船底离水面的距离)为6.5m,如果该船希望在同—天内安全进出港,请问该船在什么时间段能够安全进港?它同一天内最多能在港内停留多少小时?(忽略进 出港所需的时间).