题目内容
【题目】已知椭圆![]() :
: ![]() 的长轴长为
的长轴长为![]() ,且椭圆
,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)经过原点作直线![]() (不与坐标轴重合)交椭圆于
(不与坐标轴重合)交椭圆于![]() ,
, ![]() 两点,
两点, ![]() 轴于点
轴于点![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,求证:
,求证: ![]() ,
, ![]() ,
, ![]() 三点共线..
三点共线..
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据题意列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() , ,求出
, ,求出![]() 、
、![]() 、
、![]() ,即可得结果;(2)设
,即可得结果;(2)设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
因为点![]() ,
, ![]() 都在椭圆
都在椭圆![]() 上,所以
上,所以 ,利用“点差法”证明
,利用“点差法”证明![]()
![]() ,即可得结论.
,即可得结论.
试题解析:(1)由题意得![]() ,则
,则![]() .
.
由椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() ,
,
其长度等于圆![]() 的直径,
的直径,
可得椭圆![]() 经过点
经过点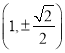 ,
,
所以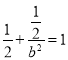 ,解得
,解得![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
因为点![]() ,
, ![]() 都在椭圆
都在椭圆![]() 上,所以
上,所以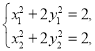
所以![]()
![]() ,
,
即![]() .
.
又![]()
![]() ,
,
所以![]() ,
,
即![]() ,
,
所以![]()
所以![]()
又![]()
![]() ,
,
所以![]() ,
,
所以![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.

练习册系列答案
相关题目