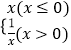题目内容
【题目】已知（ 
﹣ 
）n的展开式中，第三项的系数为144．
（1）求该展开式中所有偶数项的二项式系数之和；
（2）求该展开式的所有有理项．
【答案】
（1）解：（ 
﹣ 
）n的展开式的通项为Tr+1=Cnr（﹣2）r 
，（0≤r≤n，且r∈N）．
由题意可知：第三项的系数为Cn2（﹣2）2=144，
即n（n﹣1）=72，解得n=9．
∴该展开式中所有偶数项的二项式系数之和为28=256．
（2）解：∵（ ﹣ ）9的展开式的通项为Tr+1=C9r（﹣2）r 
，（0≤r≤9，且r∈N）．
要求该展开式中的有理项，只需令 
∈Z，
∴r=0，3，6，9，
∴展开式中的有理项为：T1=C90（﹣2）0x3=x3；T4=C93（﹣2）3x﹣1=﹣672x﹣1；
T7=C96（﹣2）6x﹣5=﹣5376x﹣5；T10=C99（﹣2）9x﹣9=﹣512x﹣9
【解析】（1）依题意，利用二项式的通项公式可求得n的值；（2）只需令 ∈Z，r=0，3，6，9，从而可求得展开式中的有理项．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
