题目内容
【题目】已知平行四边形ABCD（如图1），AB=4，AD=2，∠DAB=60°，E为AB的中点，把三角形ADE沿DE折起至A1DE位置，使得A1C=4，F是线段A1C的中点（如图2）．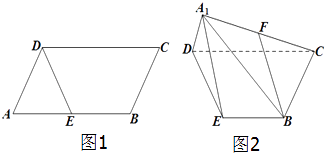 
（1）求证：BF∥面A1DE；
（2）求证：面A1DE⊥面DEBC；
（3）求二面角A1﹣DC﹣E的正切值．
【答案】
（1）证明：如图，取DA1的中点G，连FG，GE；
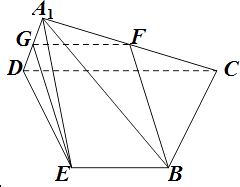F为A1C中点；
∴GF∥DC，且 
；
∴四边形BFGE是平行四边形；
∴BF∥EG，EG平面A1DE，BF平面A1DE；
∴BF∥平面A1DE
（2）证明：如图，取DE的中点H，连接A1H，CH；
AB=4，AD=2，∠DAB=60°，E为AB的中点；
∴△DAE为等边三角形，即折叠后△DA1E也为等边三角形；
∴A1H⊥DE，且 
；
在△DHC中，DH=1，DC=4，∠HDC=60°；
根据余弦定理，可得：
HC2=1+16﹣4=13，在△A1HC中， ， 
，A1C=4；
∴ 
，即A1H⊥HC，DE∩HC=H；
∴A1H⊥面DEBC；
又A1H面A1DE；
∴面A1DE⊥面DEBC；
（3）解：如上图，过H作HO⊥DC于O，连接A1O；
A1H⊥面DEBC；
∴A1H⊥DC，A1H∩HO=H；
∴DC⊥面A1HO；
∴DC⊥A1O，DC⊥HO；
∴∠A1OH是二面角A1﹣DC﹣E的平面角；
在Rt△A1HO中， ， 
；
故tan 
；
所以二面角A1﹣DC﹣E的正切值为2．
【解析】（1）取A1D中点G，并连接FG，EG，能够说明四边形BFGE为平行四边形，从而根据线面平行的判定定理即可得出BF∥面A1DE；（2）先根据已知的边、角值说明△A1DE为等边三角形，然后取DE中点H，连接CH，从而得到A1H⊥DE，根据已知的边角值求出A1H，CH，得出 
，从而得到A1H⊥CH，从而根据线面垂直及面面垂直的判定定理即可证出面A1DE⊥面DEBC；（3）过H作HO⊥DC，垂足为O，并连接A1O，容易说明DC⊥面A1HO，从而得出∠A1OH为二面角A1﹣DC﹣E的平面角，能够求出HO，从而求出tan∠A1OH，即求出了二面角A1﹣DC﹣E的正切值．
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本，需要知道平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一个平面过另一个平面的垂线，则这两个平面垂直．
