题目内容
已知函数f(x)=x2+(a+2)x+b,满足f(-1)=-2;
(1)若方程f(x)=2x有唯一的解,求实数a,b的值;
(2)若函数f(x)在区间[-3,2]上不是单调函数,求实数a的取值范围.
(1)若方程f(x)=2x有唯一的解,求实数a,b的值;
(2)若函数f(x)在区间[-3,2]上不是单调函数,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)由f(-1)=-2可得a=b+1 ①,而由f(x)=2x有唯一解得,△=a2-4b=0 ②,所以联立①②即可得到a,b;
(2)根据f(x)在区间[-3,2]上不是单调函数,便得抛物线顶点在[-3,2]之间,也就是-3<-
<2,所以解该不等式即得a的取值范围.
(2)根据f(x)在区间[-3,2]上不是单调函数,便得抛物线顶点在[-3,2]之间,也就是-3<-
| a+2 |
| 2 |
解答:
解:(1)由f(-1)=-2得,1-a-2+b=-2,即a=b+1 ①;
由f(x)=2x得,x2+ax+b=0,该方程有唯一解;
∴△=a2-4b=0 ②;
∴由①②解得:a=2,b=1;
(2)f(x)为二次函数,对称轴为x=-
;
∵f(x)在区间[-3,2]上不是单调函数;
∴-3<-
<2,解得:-6<a<4;
∴实数a的取值范围为(-6,4).
由f(x)=2x得,x2+ax+b=0,该方程有唯一解;
∴△=a2-4b=0 ②;
∴由①②解得:a=2,b=1;
(2)f(x)为二次函数,对称轴为x=-
| a+2 |
| 2 |
∵f(x)在区间[-3,2]上不是单调函数;
∴-3<-
| a+2 |
| 2 |
∴实数a的取值范围为(-6,4).
点评:考查一元二次方程解的情况和判别式△的关系,二次函数的对称轴,以及二次函数的单调性.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
设a=0.22,b=20.2,c=1g(a+b-1),则a、b、c的大小关系为( )
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、b>a>c |
已知向量|
|=
,|
|=2,
与
的夹角为30°,则|
-
|的值( )
| AB |
| 3 |
| AC |
| AB |
| AC |
| AC |
| AB |
| A、1 | ||
| B、13 | ||
C、
| ||
D、2-
|
如果函数y=f(x)的图象经过点(0,1),那么函数y=f-1(x)+2的反函数的图象过点( )
| A、(3,0) |
| B、(0,3) |
| C、(1,2) |
| D、(2,1) |
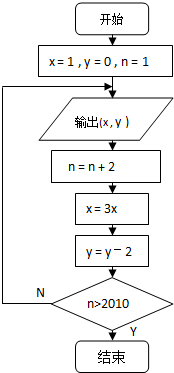 已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…
已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…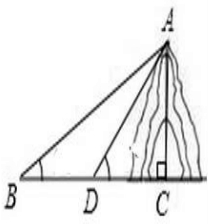 如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°=
如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°=