题目内容
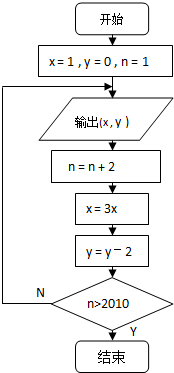 已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…
已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…(Ⅰ)若程序运行中输出的一个数组是(9,t),则t=
(Ⅱ)程序结束时,共输出(x,y )的组数为
(Ⅲ)写出流程图的程序语句.
考点:程序框图
专题:算法和程序框图
分析:按照程序框图的流程写出前几次循环的结果,得到点符合的特征为(3n,-2n),令横坐标为9,求出纵坐标;得到n为奇数,当满足判断框中的条件时出现的奇数个数即共输出(x,y)的组数.
解答:
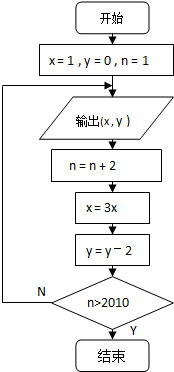 (本小题满分12分)
(本小题满分12分)
解:(Ⅰ)由已知中的程序框图,我们可得:
当n=1时,输出(1,0),然后n=3,x=3,y=-2;
当n=3时,输出(3,-2),然后n=5,x=32=9,y=-2×2=-4;
当n=5时,输出(9,-4),然后n=7,x=33=27,y=-2×3=-6;
故t=-4.
故答案为:-4 (3分)
(Ⅱ)由(I)可知
程序循环变量n的初值为1,终值为2011,步长为2
故循环共执行(2011-1)÷2+1=1006次
故答案为:1006 (7分)
(Ⅲ)流程图的程序语句如下:
x=1
y=0
n=1
DO
INPUT(x,y)
n=n+2
x=3x
y=y-2
LOOP UNTIL n>2010
END(12分)
 (本小题满分12分)
(本小题满分12分)解:(Ⅰ)由已知中的程序框图,我们可得:
当n=1时,输出(1,0),然后n=3,x=3,y=-2;
当n=3时,输出(3,-2),然后n=5,x=32=9,y=-2×2=-4;
当n=5时,输出(9,-4),然后n=7,x=33=27,y=-2×3=-6;
故t=-4.
故答案为:-4 (3分)
(Ⅱ)由(I)可知
程序循环变量n的初值为1,终值为2011,步长为2
故循环共执行(2011-1)÷2+1=1006次
故答案为:1006 (7分)
(Ⅲ)流程图的程序语句如下:
x=1
y=0
n=1
DO
INPUT(x,y)
n=n+2
x=3x
y=y-2
LOOP UNTIL n>2010
END(12分)
点评:本题考查解决程序框图中的循环结构时,常采用利用框图的流程写出前几次循环的结果,找规律,本题属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设全集I=R,集合A={y|y=x2-2},B={x|y=log2(3-x)},则(∁IA)∩B等于( )
| A、{x|-2≤x<3} |
| B、{x|x≤-2} |
| C、{x|x<3} |
| D、{x|x<-2} |
设F1,F2为双曲线C:
-
=1(a>0,b>0)的左、右焦点,过坐标原点O的直线与双曲线C在第一象限内交于点P,若|PF1|+|PF2|=6a,且△PF1F2为锐角三角形,则直线OP斜率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||||||
B、(
| ||||||
C、(1,
| ||||||
D、(
|