题目内容
设a=0.22,b=20.2,c=1g(a+b-1),则a、b、c的大小关系为( )
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、b>a>c |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用指数函数、对数函数的单调性求解.
解答:
解:∵0<a=0.22<0.20=1,
b=20.2>20=1,
c=1g(a+b-1)<lg1=0,
∴b>a>c.
故选:D.
b=20.2>20=1,
c=1g(a+b-1)<lg1=0,
∴b>a>c.
故选:D.
点评:本题考查三个数的大小的比较,是基础题,解题时要注意指数函数、对数函数的单调性的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设有直线a,b,c,d及平面α,β,下列条件能推出α∥β的是( )
| A、a?α,b?β,a∥b,c?α,d?β,c∥d |
| B、a?α,b?β,a∥β,b∥α |
| C、a⊥α,b⊥β,a∥b |
| D、平面α内有三个不共线的点到β距离相等 |
若sin(π-α)=-2sin(
+α),则sinα•cosα=( )
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
| ∫ |
-
|
| A、0 | ||
B、-
| ||
C、
| ||
| D、π |
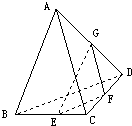 E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )
E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )