题目内容
已知抛物线C的顶点在原点，经过点A（1，2），其焦点F在y轴上，直线y=kx+2交抛物线C于A，B两点，M是线段AB的中点，过M作x轴的垂线交抛物线C于点N．
（Ⅰ）求抛物线C的方程；
（Ⅱ）证明：抛物线C在点N处的切线与AB平行．
（Ⅰ）求抛物线C的方程；
（Ⅱ）证明：抛物线C在点N处的切线与AB平行．
依题意，设抛物线C的方程为y=ax2，
（Ⅰ）∵点A（1，2）在抛物线C上，∴a=1．
∴抛物线C的方程为y=2x2．…（4分）
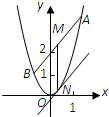
（Ⅱ）如图，设A（x1，2x12），B（x2，2x22），
把y=kx+2代入y=2x2得：2x2-kx-2=0，
由韦达定理得：x1+x2=
，x1x2=-1，∴xN=xM=
=
，
即N点的坐标为（
，
）．…（8分）
设抛物线在点N处的切线l的方程为y-
=m（x-
），
将y=2x2代入上式得：2x2-mx+
-
=0，
∵直线l与抛物线C相切，所以△=m2-8（
-
）=m2-2mk+k2=（m-k）2=0，
∴m=k，即l∥AB．…（12分）
（Ⅰ）∵点A（1，2）在抛物线C上，∴a=1．
∴抛物线C的方程为y=2x2．…（4分）
（Ⅱ）如图，设A（x1，2x12），B（x2，2x22），
把y=kx+2代入y=2x2得：2x2-kx-2=0，
由韦达定理得：x1+x2=
| k |
| 2 |
| x1+x2 |
| 2 |
| k |
| 4 |
即N点的坐标为（
| k |
| 4 |
| k2 |
| 8 |
设抛物线在点N处的切线l的方程为y-
| k2 |
| 8 |
| k |
| 4 |
将y=2x2代入上式得：2x2-mx+
| mk |
| 4 |
| k2 |
| 8 |
∵直线l与抛物线C相切，所以△=m2-8（
| mk |
| 4 |
| k2 |
| 8 |
∴m=k，即l∥AB．…（12分）
练习册系列答案
新思维寒假作业系列答案
相关题目
