题目内容

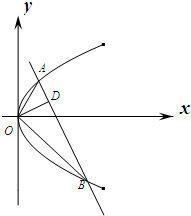
如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点（1，
3
2
）到F1、F2两点的距离之和为4．
（1）求椭圆C的方程和焦点坐标；
（2）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求弦长|PQ|．
（1）由题设知：2a=4，即a=2，
将点（1，
3
2
）代入椭圆方程得
1
22
+
(
3
2
)2
b2
=1，
解得b2=3
∴c2=a2-b2=4-3=1，故椭圆方程为
x2
4
+
y2
3
=1，
焦点F1、F2的坐标分别为（-1，0）和（1，0）
（2）由（Ⅰ）知A（-2，0），B（0，
3
），∴kPQ=kAB=
3
2
，
∴PQ所在直线方程为y=
3
2
（x-1），
由
y=
3
2
(x-1)
x2
4
+
y2
3
=1
得2x2-2x-3=0，
设P（x1，y1），Q（x2，y2），则x1+x2=1，x1-x2=-
3
2
，
弦长|PQ|=
1+k2
(x1+x2)2-4x1x2
=
7
2
•
7
=
7
2
．
练习册系列答案
相关题目
已知点M是曲线C上任一点，点M到点F（1，0）的距离比到y轴的距离多1．
（1）求曲线C的方程；
（2）过点P（0，2）的直线L交曲线C于A、B两点，若以AB为直径的圆经过原点O，求直线L的方程．
椭圆
x2
16
+
y2
9
=1的左、右焦点分别为F1、F2，过焦点F1的直线交椭圆于A，B两点，若△ABF2的内切圆的面积为π．A，B两点的坐标分别为（x1，y1）和（x2，y2），则|y2-y1|的值为______．
已知抛物线C的顶点在原点，经过点A（1，2），其焦点F在y轴上，直线y=kx+2交抛物线C于A，B两点，M是线段AB的中点，过M作x轴的垂线交抛物线C于点N．
（Ⅰ）求抛物线C的方程；
（Ⅱ）证明：抛物线C在点N处的切线与AB平行．
如图，抛物线C1：y2=8x与双曲线C2：
x2
a2
-
y2
b2
=1(a＞0，b＞0)有公共焦点F2，点A是曲线C1，C2在第一象限的交点，且|AF2|=5．
（Ⅰ）求双曲线C2的方程；
（Ⅱ）以F1为圆心的圆M与双曲线的一条渐近线相切，圆N：（x-2）2+y2=1．平面上有点P满足：存在过点P的无穷多对互相垂直的直线l1，l2，它们分别与圆M，N相交，且直线l1被圆M截得的弦长与直线l2被圆N截得的弦长的比为
3
：1，试求所有满足条件的点P的坐标．
如图：已知直线与抛物线y2=2px（p＞0）交于A，B两点，且OA⊥OB，OD⊥AB交AB于点D，点D的坐标为（2，1）．
（1）求p的值；
（2）求△AOB的面积．
已知直线与椭圆
x2
9
+
y2
4
=1交于A，B两点，设线段AB的中点为P，若直线的斜率为k1，直线OP的斜率为k2，则k1k2等于______．
直线l：y=k(x-
2
)与双曲线x2-y2=1仅有一个公共点，则实数k的值为（　　）
A．1B．-1C．1或-1D．1或-1或0
如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点(1，
3
2
)到F1、F2两点的距离之和为4．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求△F1PQ的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网