题目内容

9．若函数f（x），g（x）分别是R上的奇函数、偶函数，且满足f（x）+g（x）=e-z，则有（　　）
A．g（1）＜g（2）＜f（0）B．f（0）＜g（2）＜g（1）C．g（1）＜f（0）＜g（2）D．f（0）＜g（1）＜g（2）

分析 先由已知f（x）+g（x）=e-x，及f（-x）=-f（x），g（-x）=g（x），可求出f（x），g（x），进而可比较f（0），g（1），g（2）的大小．

解答 解：∵函数f（x），g（x）分别是R上的奇函数、偶函数，
∴f（-x）=-f（x），g（-x）=g（x），
又∵f（x）+g（x）=e-x，①
∴f（-x）+g（-x）=-f（x）+g（x）=ex，②
由①②得f（x）=$\frac{1}{2}$（e-x-ex），g（x）=$\frac{1}{2}$（e-x+ex），
∴f（0）=0，
g（1）=$\frac{1}{2}$（e+e-1），
g（2）=$\frac{1}{2}$（e-2+e2），
故f（0）＜g（1）＜g（2），
故选：D

点评 本题主要考查奇偶性的在求解析式中的应用，也考查了方程思想．

练习册系列答案
相关题目
19．已知函数f（x）=ax3+|x-a|，a∈R  若a=-1，求函数y=f（x）的图象在x=1处的切线方程．
20．已知幂函数y=xn，y=xm，y=xp的图象如图，则（　　）
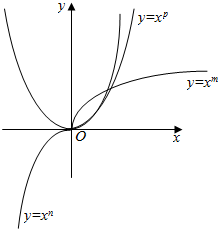
A．m＞n＞pB．m＞p＞nC．n＞p＞mD．p＞n＞m
17．已知点A（-4，0）、P（t，0）（t＞0），在第一象限作正方形OPQR，过A、P、Q三点作⊙B，连接OQ，作CQ⊥OQ交圆于点C，连接OB、AQ．
（1）求证：∠CQP=∠AOQ；
（2）CQ的长度是否随着t的变化而变化？如果变化，请用含t的代数式表示CQ的长度，如果不变，求出CQ的长；
（3）当tan∠AQO=$\frac{1}{2}$时，
①求点C的坐标；
②点D是⊙B上的任意一点，求CD+$\sqrt{5}$OD的最小值．
4．如果2cosx-1=0，x∈[0，2π]，则x=$\frac{π}{3}$或$\frac{5π}{3}$．
14．已知函数f（x）=asinωx+bcosωx，其中ab≠0．
（1）已知ω=2，且函数y=f（x）的图象经过点（$\frac{π}{4}$，2）和点（$\frac{π}{2}$，-2）．
①求y=f（x）的解析式；
②将函数y=f（x）的图象上各点的横坐标保持不变，纵坐标缩短为原来的$\frac{\sqrt{2}}{2}$倍，再把所得图象向右平移$\frac{π}{4}$个单位，得到函数y=g（x）的图象，若方程g（|x|）=m在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上有且只有2个不同的实根，求实数m的取值范围．
（2）已知ω=1，且函数y=f（x）在x=x0处取最大值，当实数a，b满足（a-$\sqrt{3}$）2+（b-1）2=1时，求tan（$\frac{π}{4}$-x0）的取值范围．
1．已知f（x）是定义在R上的奇函数，且是周期为2的周期函数，当x∈[0，1）时，f（x）=2x-1，则f（log${\;}_{\frac{1}{2}}$6）=-$\frac{1}{2}$．
18．已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=x（1-x），求
（1）f（0）；
（2）当x＜0时，f（x）的表达式；
（3）f（x）的表达式．
19．求方程x5+10x3+20x-4=0的实数根（精确到0.01）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网