Question

14．已知函数f（x）=asinωx+bcosωx，其中ab≠0．
（1）已知ω=2，且函数y=f（x）的图象经过点（$\frac{π}{4}$，2）和点（$\frac{π}{2}$，-2）．
①求y=f（x）的解析式；
②将函数y=f（x）的图象上各点的横坐标保持不变，纵坐标缩短为原来的$\frac{\sqrt{2}}{2}$倍，再把所得图象向右平移$\frac{π}{4}$个单位，得到函数y=g（x）的图象，若方程g（|x|）=m在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上有且只有2个不同的实根，求实数m的取值范围．
（2）已知ω=1，且函数y=f（x）在x=x₀处取最大值，当实数a，b满足（a-$\sqrt{3}$）²+（b-1）²=1时，求tan（$\frac{π}{4}$-x₀）的取值范围．

Answer 1

分析 （1）①由ω=2，再根据f（x）的图象经过点（$\frac{π}{4}$，2）和点（$\frac{π}{2}$，-2），求得a，b的值，代入后利用辅助角公式整理得答案；
②由已知的伸缩变换和平移变换得到函数g（x）的图象，画出图形，数形结合得到满足条件的m的范围；
（2）由f（x）=asinx+bcosx=$\sqrt{{a}^{2}+{b}^{2}}sin（x+θ）$（tanθ=$\frac{b}{a}$），可得${x}_{0}=\frac{π}{2}+2kπ-θ，k∈Z$，由直线和圆相切求得tanθ=$\frac{b}{a}$∈[0，$\sqrt{3}$]，则0$≤θ≤\frac{π}{3}$．
代入tan（$\frac{π}{4}$-x₀）整理后可得tan（$θ-\frac{π}{4}$）的范围．

解答 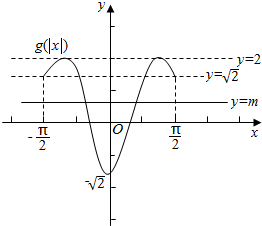解：（1）①由ω=2，可得f（x）=asin2x+bcos2x，再根据f（x）的图象经过点（$\frac{π}{4}$，2）和点（$\frac{π}{2}$，-2），
可得 a=2，-b=-2，即a=2，b=2，∴f（x）=2sin2x+2cos2x=2$\sqrt{2}$sin（2x+$\frac{π}{4}$）．
②将函数y=f（x）的图象上各点的横坐标保持不变，纵坐标缩短为原来的$\frac{\sqrt{2}}{2}$倍，可得y=2sin（2x+$\frac{π}{4}$）的图象；
再把所得图象向右平移$\frac{π}{4}$个单位，得到函数g（x）=2sin[2（x-$\frac{π}{4}$）+$\frac{π}{4}$]=2sin（2x-$\frac{π}{4}$） 的图象，
若方程g（|x|）=m在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上有且只有2个不同的实根，
则g（|x|）=2sin（2|x|-$\frac{π}{4}$）的图象和直线y=m在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上有且只有2个交点，如图．
故-$\sqrt{2}$＜m＜$\sqrt{2}$，或 m=2．
（2）∵已知ω=1，故f（x）=asinx+bcosx=$\sqrt{{a}^{2}+{b}^{2}}sin（x+θ）$（tanθ=$\frac{b}{a}$），
∴当$x+θ=\frac{π}{2}+2kπ，k∈Z$，即$x=\frac{π}{2}+2kπ-θ，k∈Z$时f（x）取得最大值．
由函数y=f（x）在x=x₀处取最大值，∴${x}_{0}=\frac{π}{2}+2kπ-θ，k∈Z$．
当实数a，b满足（a-$\sqrt{3}$）²+（b-1）²=1时，点A（a，b）在以C（$\sqrt{3}$，1）为圆心，半径等于1的圆上，
设过原点的直线方程为y=kx，由点C（$\sqrt{3}$，1）到直线kx-y=0的距离等于1，得$\frac{|\sqrt{3}k-1|}{\sqrt{{k}^{2}+1}}=1$，解得k=0或k=$\sqrt{3}$．
∴tanθ=$\frac{b}{a}$∈[0，$\sqrt{3}$]，则0$≤θ≤\frac{π}{3}$．
∴tan（$\frac{π}{4}$-x₀）=tan（$\frac{π}{4}$-$\frac{π}{2}-2kπ+θ$）=tan（$θ-\frac{π}{4}$），
∵0$≤θ≤\frac{π}{3}$，∴$-\frac{π}{4}≤θ-\frac{π}{4}≤\frac{π}{12}$，
则tan（$θ-\frac{π}{4}$）∈[-1，2$-\sqrt{3}$]．

点评 本题考查y=Asin（ωx+φ）型函数的图象和性质，考查了三角函数的图象平移问题，考查数形结合的解题思想方法和数学转化思想方法，对于（2）的求解，正确理解题意是关键，属中高档题．