题目内容
已知圆C的圆心在直线l1:x-y-1=0上，圆C与直线l2:4x+3y+14=0相切，并且圆C截直线l3:3x+4y+10=0所得弦长为6，求圆C的方程.
所求圆C的方程为(x－2)2+(y-1)2＝25.
设圆的方程为(x－a)2+(y－ｂ)2＝ｒ2(r＞0).
∵圆心在直线x-y-1=0上，
∴a-b-1="0. " ①
又∵圆C与直线l2相切，
∴|4a+3b+14|="5r. " ②
∵圆C截直线l3所得弦长为6，
∴(
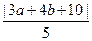)2+32=r2. ③
解①②③组成的方程组得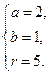
∴所求圆C的方程为(x－2)2+(y-1)2＝25.
∵圆心在直线x-y-1=0上，
∴a-b-1="0. " ①
又∵圆C与直线l2相切，
∴|4a+3b+14|="5r. " ②
∵圆C截直线l3所得弦长为6，
∴(
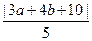)2+32=r2. ③解①②③组成的方程组得
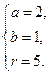
∴所求圆C的方程为(x－2)2+(y-1)2＝25.
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
（1）设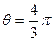
时对应的点这P，求直线OP的倾斜角；（2）若此圆经过点（m,1），求m的值，其中
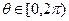；（3）求圆上点到直线
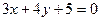距离的最值．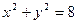
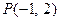
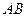
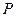
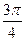时，求弦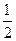
=0与圆(x-cosβ)2+(y+sinβ)2=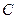
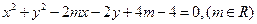
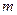的值，使圆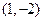
的直线方程．
取最大值时，点P的横坐标为_______________。
与圆
交于
两点，则当
的面积最大时，
_______