题目内容
17.若函数f(x)=Acos($\frac{π}{2}$x+φ)(A>0),满足f(1)=0,则( )| A. | f(x)在[0,1]上单调递增 | B. | f(x)在[0,1]上单调递减 | ||
| C. | f(x+3)一定是偶函数 | D. | f(x+3)一定是奇函数 |
分析 由条件利用诱导公式化简函数的解析式,再利用余弦函数的奇偶性,得出结论.
解答 解:由于f(1)=Acos($\frac{π}{2}$+φ)=-Asinφ=0,故可取φ=kπ,k∈Z,∴函数f(x)=Acos($\frac{π}{2}$x+kπ)=±Acos$\frac{π}{2}$x(A>0),
故函数f(x)在[0,1]上的单调性不确定,故排除A、B.
再根据f(x+3)=±Acos$\frac{π}{2}$(x+3)=±Asin$\frac{π}{2}$x,可得f(x+3)一定是奇函数,
故选:D.
点评 本题主要考查诱导公式、余弦函数的奇偶性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.某工厂有400名工人,现采用系统抽样的方法抽取40人作问卷调查,将400人按1,2,…,400随机编号,则抽取的40人中,编号落入区间[81,190]的人数为( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
6.下列函数中,周期为$\frac{π}{2}$,且在[$\frac{π}{8}$,$\frac{π}{4}$]上为减函数的是( )
| A. | y=sin(4x+$\frac{π}{2}$) | B. | y=cos(4x+$\frac{π}{2}$) | C. | y=sin(2x+$\frac{π}{2}$) | D. | y=cos(2x+$\frac{π}{2}$) | ||||
| E. | y=cos(4x+$\frac{π}{2}$) |
7.集合P={x|x=$\frac{2k-1}{4}$,k∈Z},Q={y|y=$\frac{k+2}{4}$,k∈Z},则有( )
| A. | P=Q | B. | P?Q | C. | P?Q | D. | P∩Q=∅ |
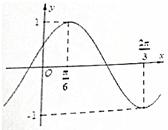 已知函数f(x)=Asin(ωx+φ),其中(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ),其中(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.