Question

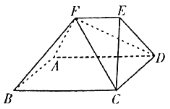
【题目】如图，在多面体中，底面是正方形，梯形底面，且．

（Ⅰ）证明平面平面；

（Ⅱ）平面将多面体分成两部分，求两部分的体积比．

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ）．

【解析】

（Ⅰ）取的中点，连接，可得，，即可得平面，从而证明平面平面；

（Ⅱ）作于，过作于，作，．

利用多面体的体积，求得多面体的体积，进而求得，得到答案．

（Ⅰ）由题意，多面体的底面是正方形，可得，

又由梯形底面，梯形底面，

平面，所以平面，

因为平面，所以，

因为梯形中，，

取的中点，连接，所以，所以，

又因为，所以平面，

又由平面，所以平面平面．

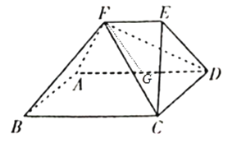
（Ⅱ）如图所示，作于，过作于，作，．

∵梯形底面，且．

∴面，面，

在中，由可得，

令，

则，，

多面体的体积为：．

由（1）及对称性可得平面，

∵，，∴到面的距离等于到面的距离的一半，

即到面的距离等于，

故．

∴平面将多面体分成两部分，两部分的体积比为．