题目内容
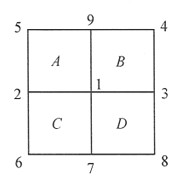
【题目】设n为正整数,称n×n的方格表Tn的网格线的交点(共(n+1)2个交点)为格点.现将数1,2,……,(n+1)2分配给Tn的所有格点,使不同的格点分到不同的数.称Tn的一个1×1格子S为“好方格”,如果从2S的某个顶点起按逆时针方向读出的4个顶点上的数依次递增(如图是将数1,2,…,9分配给T2的格点的一种方式,其中B、C是好方格,而A、D不是好方格)设Tn中好方格个数的最大值为f(n).
(1)求f(2)的值;
(2)求f(n)关于正整数n的表达式.
【答案】(1)f(2)=3.(2)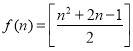 .
.
【解析】
(1)如图①,将T2的4个1×1格子(以下简称“格子”)分别记为A、B、C、D,将9个格点上的数分别记为a、b、c、d、e、f、g、h、i.
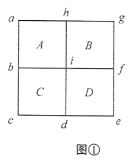
当a,b,……,i依次取为1,2,……,9时,易验证B、C、D均为好方格,这表明f(2)≥3.
现假设f(2)=4,即存在一种数的分配方式,使A、B、C、D均为好方格.
由对称性,不妨设边界上8个数a,b,……,h中的最小数为a或b.此时由A为好方格知,或者有a<b<i<h,或者有b<i<h<a,故b<i<h总是成立的.进而由B、C为好方格知,必有i<f<g<h,b<c<d<i,但这时d<i<f,与D为好方格矛盾.
综上可得f(2)=3.
(2)设Tn的各格点的数已被分配好,此时好方格有k个称格子的一条边为一段“格线”我们对Tn的每段格线标记一个箭头若格线连结了两个格点U、V,其中U上的数小于V上的数,则对格线UV标上一个指向![]() 顺时针旋转90°后所得方向的箭头.
顺时针旋转90°后所得方向的箭头.
称一个格子S及S的一条边UV所构成的有序对(S,UV)为一个“对子”,如果UV上所标的箭头由S内指向S外设对子总数为N.
一方面,每个格子S至少贡献1个对子(否则沿逆时针方向读S顶点上的数将永远递减,矛盾),而根据好方格的定义每个好方格贡献3个对子,于是![]() .
.
另一方面,Tn的每段格线至多贡献1个对子,且Tn边界上至少有一段格线标有向内的箭头(否则,沿逆时针方向读n边界上的数将永远递增,矛盾),从而不贡献对子.注意到Tn的格线段数为2n(n+1),所以又有![]() .
.
综合两方面得,2k+n2≤2n(n+1)-1,即好方格的个数![]() .
.
最后,对n为奇数和n为偶数的情况,分别如图②和图③,将1,2,……,(n+1)2按粗线经过的次序依次分配给所有格点对图中标有“▲”记号的每个格子,易验证,按被粗线经过的先后次序排列其4个顶点,恰是一种逆时针排列,因而这些格子均为好方格.
图②中好方格数为![]() .
.
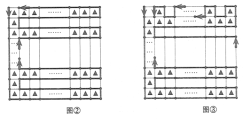
图③中好方格数为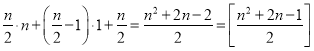 .
.
综上可得,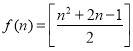 .
.