题目内容
(2012•香洲区模拟)已知数列{an}是各项均不为0的等差数列,公差为d,Sn为其前 n项和,且满足
=S2n-1,n∈N*.数列{bn}满足bn=
,Tn为数列{bn}的前n项和.
(1)求数列{an}的通项公式an和数列{bn}的前n项和Tn;
(2)若对任意的n∈N*,不等式λTn<n+8•(-1)n恒成立,求实数λ的取值范围;
(3)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
| a | 2 n |
| 1 |
| an•an+1 |
(1)求数列{an}的通项公式an和数列{bn}的前n项和Tn;
(2)若对任意的n∈N*,不等式λTn<n+8•(-1)n恒成立,求实数λ的取值范围;
(3)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
分析:(1)在
=S2n-1中,令n=1,n=2,即可求得数列的通项,利用裂项法,可求Tn;
(2)分n为偶数、奇数时,利用分离参数法,通过求函数的最值,即可确定λ的取值范围;
(3)利用等比数列的性质可得(
)2=
(
),进一步可得
=
>0,由此可得结论.
| a | 2 n |
(2)分n为偶数、奇数时,利用分离参数法,通过求函数的最值,即可确定λ的取值范围;
(3)利用等比数列的性质可得(
| m |
| 2m+1 |
| 1 |
| 3 |
| n |
| 2n+1 |
| 3 |
| n |
| -2m2+4m+1 |
| m2 |
解答:解:(1)在
=S2n-1中,令n=1,n=2,
得
,即
…(1分)
解得a1=1,d=2,∴an=2n-1
又∵an=2n-1时,Sn=n2满足
=S2n-1,∴an=2n-1…(2分)
∵bn=
=
(
-
),
∴Tn=
(1-
+
-
+…+
-
)=
. …(4分)
(2)①当n为偶数时,要使不等式λTn<n+8•(-1)n恒成立,即需不等式λ<
=2n+
+17恒成立. …(5分)
∵2n+
≥8,等号在n=2时取得.
∴此时λ 需满足λ<25. …(6分)
②当n为奇数时,要使不等式λTn<n+8•(-1)n恒成立,即需不等式λ<
=2n-
-15恒成立. …(7分)
∵2n-
是随n的增大而增大,∴n=1时,2n-
取得最小值-6.
∴此时λ 需满足λ<-21. …(8分)
综合①、②可得λ的取值范围是λ<-21. …(9分)
(3)T1=
, Tm=
, Tn=
,
若T1,Tm,Tn成等比数列,则(
)2=
(
),
即
=
. …(10分)
由
=
,可得
=
>0,即-2m2+4m+1>0,
∴1-
<m<1+
. …(11分)
又m∈N,且m>1,所以m=2,此时n=12…(12分)
因此,当且仅当m=2,n=12时,数列T1,Tm,Tn中的T1,Tm,Tn成等比数列.…(13分)
| a | 2 n |
得
|
|
解得a1=1,d=2,∴an=2n-1
又∵an=2n-1时,Sn=n2满足
| a | 2 n |
∵bn=
| 1 |
| an•an+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
(2)①当n为偶数时,要使不等式λTn<n+8•(-1)n恒成立,即需不等式λ<
| (n+8)(2n+1) |
| n |
| 8 |
| n |
∵2n+
| 8 |
| n |
∴此时λ 需满足λ<25. …(6分)
②当n为奇数时,要使不等式λTn<n+8•(-1)n恒成立,即需不等式λ<
| (n-8)(2n+1) |
| n |
| 8 |
| n |
∵2n-
| 8 |
| n |
| 8 |
| n |
∴此时λ 需满足λ<-21. …(8分)
综合①、②可得λ的取值范围是λ<-21. …(9分)
(3)T1=
| 1 |
| 3 |
| m |
| 2m+1 |
| n |
| 2n+1 |
若T1,Tm,Tn成等比数列,则(
| m |
| 2m+1 |
| 1 |
| 3 |
| n |
| 2n+1 |
即
| m2 |
| 4m2+4m+1 |
| n |
| 6n+3 |
由
| m2 |
| 4m2+4m+1 |
| n |
| 6n+3 |
| 3 |
| n |
| -2m2+4m+1 |
| m2 |
∴1-
| ||
| 2 |
| ||
| 2 |
又m∈N,且m>1,所以m=2,此时n=12…(12分)
因此,当且仅当m=2,n=12时,数列T1,Tm,Tn中的T1,Tm,Tn成等比数列.…(13分)
点评:本题考查等差数列与等比数列的定义与性质、数列求和等基础知识,考查运算求解能力、推理论证能力,考查函数与方程的思想、分类与整合的思想、转化与化归的思想.

练习册系列答案
相关题目

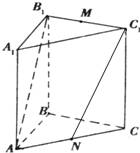 (2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.
(2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.