题目内容
（2012•香洲区模拟）如图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有n（n＞1，n∈N*）个点，相应的图案中总的点数记为an，则
+
+
+…+
=（ ）
| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| a2012a2013 |
分析：根据图象的规律可得出通项公式an，根据数列{
}的特点可用列项法求其前n项和的公式，而
+
+
+…+
是前2011项的和，代入前n项和公式即可得到答案．
| 9 |
| anan+1 |
| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| a2012a2013 |
解答：解：每个边有n个点，把每个边的点数相加得3n，这样角上的点数被重复计算了一次，故第n个图形的点数为3n-3，即an=3n-3．
令Sn=
+
+
+…+
=
+
+…+
=1-
+
-
+…+
-
=
∴
+
+
+…+
=
故选B．
令Sn=
| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| anan+1 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (n-1)n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| n-1 |
| n |
∴
| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| a2012a2013 |
| 2011 |
| 2012 |
故选B．
点评：本题主要考查简单的和清推理，求等差数列的通项公式和用裂项法对数列进行求和问题，同时考查了计算能力，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
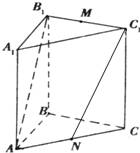（2012•香洲区模拟）如图，直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=4，BC=4，BB1=3，M、N分别是B1C1和AC的中点．