题目内容
(2012•香洲区模拟)已知椭圆C的焦点在x轴上,中心在原点,离心率e=
,直线l:y=x+2与以原点为圆心,椭圆C的短半轴为半径的圆O相切.
(I)求椭圆C的方程;
(Ⅱ)设椭圆C的左、右顶点分别为A1,A2,点M是椭圆上异于Al,A2的任意一点,设直线MA1,MA2的斜率分别为kMA1,kMA2,证明kMA1,kMA2为定值.
| ||
| 3 |
(I)求椭圆C的方程;
(Ⅱ)设椭圆C的左、右顶点分别为A1,A2,点M是椭圆上异于Al,A2的任意一点,设直线MA1,MA2的斜率分别为kMA1,kMA2,证明kMA1,kMA2为定值.
分析:(I)设椭圆的方程,利用离心率e=
,直线l:y=x+2与以原点为圆心,椭圆C的短半轴为半径的圆O相切,确定几何量,从而可得椭圆的方程;
(Ⅱ)利用M点在椭圆上,计算斜率,化简即可得到结论.
| ||
| 3 |
(Ⅱ)利用M点在椭圆上,计算斜率,化简即可得到结论.
解答:(I)解:设椭圆的方程为
+
=1(a>b>0)
∵离心率e=
,∴a2=3c2,∴b2=2c2
∵直线l:y=x+2与以原点为圆心,椭圆C的短半轴为半径的圆O相切
∴b=
=
∴c2=1
∴a2=3
∴椭圆的方程为
+
=1;
(Ⅱ)证明:由椭圆方程得A1(-
,0),A2(
,0),
设M点坐标(x0,y0),则
+
=1
∴y02=
(3-x02)
∴kMA1•kMA2=
×
=
=
=-
∴kMA1•kMA2是定值-
是定值.
| x2 |
| a2 |
| y2 |
| b2 |
∵离心率e=
| ||
| 3 |
∵直线l:y=x+2与以原点为圆心,椭圆C的短半轴为半径的圆O相切
∴b=
| 2 | ||
|
| 2 |
∴c2=1
∴a2=3
∴椭圆的方程为
| x2 |
| 3 |
| y2 |
| 2 |
(Ⅱ)证明:由椭圆方程得A1(-
| 3 |
| 3 |
设M点坐标(x0,y0),则
| x02 |
| 3 |
| y02 |
| 2 |
∴y02=
| 2 |
| 3 |
∴kMA1•kMA2=
| y0 | ||
x0+
|
| y0 | ||
x0-
|
| y02 |
| x02-3 |
| ||
| x02-3 |
| 2 |
| 3 |
∴kMA1•kMA2是定值-
| 2 |
| 3 |
点评:本题考查椭圆的标准方程,考查直线与圆相切,考查斜率的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目

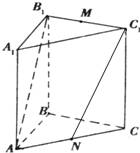 (2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.
(2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.