题目内容
(本小题满分12分)
已知椭圆的中心在原点,焦点在 轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线
轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线 在
在 轴上的截距为
轴上的截距为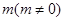 ,
, 交椭圆于A、B两个不同点.
交椭圆于A、B两个不同点.
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.
(1) (2)
(2)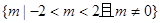 (3)设直线MA、MB的斜率分别为k1,k2,证明k1+k2=0即可.
(3)设直线MA、MB的斜率分别为k1,k2,证明k1+k2=0即可.
解析试题分析:(1)设椭圆方程为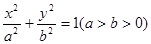 ,
,
,则 ,∴椭圆方程
,∴椭圆方程 .
.
(2)∵直线l平行于OM,且在 轴上的截距为m,又
轴上的截距为m,又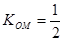 ,
,
∴l的方程为: ,
,
由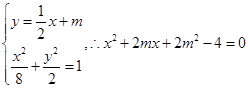 ,
,
∵直线l与椭圆交于A、B两个不同点,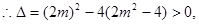
∴m的取值范围是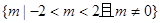
(3)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可
设
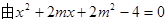 可得
可得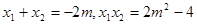
而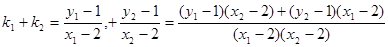

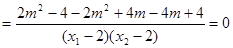 ,
,
∴k1+k2=0,故直线MA、MB与x轴始终围成一个等腰三角形.
考点:本小题主要考查椭圆方程,直线与椭圆的位置关系,椭圆的性质.
点评:本题主要考查了直线与圆锥曲线的关系的综合问题.考查了学生转化和化归思想的运用,统筹运算的能力.

练习册系列答案
相关题目
 为
为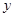 轴上的动点,点
轴上的动点,点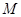 为
为 轴上的动点,点
轴上的动点,点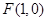 为定点,且满足
为定点,且满足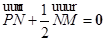 ,
,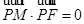 .
.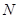 的轨迹
的轨迹 的方程;
的方程; 且斜率为
且斜率为 的直线
的直线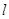 与曲线
与曲线 ,
, ,试判断在
,试判断在 ,使得
,使得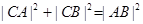 成立,请说明理由.
成立,请说明理由. ,离心率e=
,离心率e=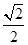 ,过右焦点F的直线l交椭圆于P、Q两点.
,过右焦点F的直线l交椭圆于P、Q两点.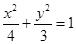 ,抛物线C2:
,抛物线C2: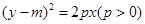 ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.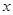 轴时,求
轴时,求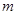 、
、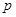 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;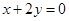 与圆
与圆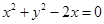 的交点为A、B,
的交点为A、B,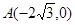 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且 ·
· ="0," |
="0," |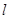 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求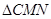 面积的最大值,并求此时直线
面积的最大值,并求此时直线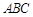 的两个顶点
的两个顶点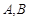 的坐标分别是
的坐标分别是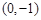 ,
,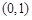 ,且
,且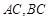 所在直线的斜率之积等于
所在直线的斜率之积等于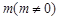 .
.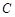 的轨迹
的轨迹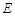 的方程,并判断轨迹
的方程,并判断轨迹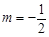 时,过点
时,过点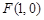 的直线
的直线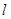 交曲线
交曲线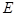 于
于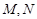 两点,设点
两点,设点 关于
关于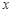 轴的对称点为
轴的对称点为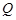 (
(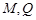 不重合).求证直线
不重合).求证直线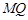 与
与 的方程为
的方程为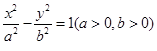 ,
,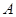 、
、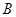 为其左、右两个顶点,
为其左、右两个顶点,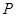 是双曲线
是双曲线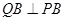 ,
,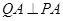 ,垂足分别为
,垂足分别为 与
与 交于点
交于点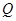 .
.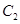 方程;
方程; 、
、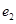 ,当
,当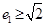 时,求
时,求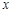 轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)  平行于
平行于 ,且与椭圆交于A、B两个不同点.
,且与椭圆交于A、B两个不同点.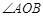 为钝角,求直线
为钝角,求直线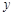 轴上的截距m的取值范围;
轴上的截距m的取值范围;