题目内容
20.已知向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-4,7),则向量$\overrightarrow{b}$在向量$\overrightarrow{a}$的方向上的投影为( )| A. | $\frac{\sqrt{13}}{13}$ | B. | $\sqrt{13}$ | C. | $\frac{\sqrt{65}}{5}$ | D. | $\sqrt{65}$ |
分析 根据投影的定义,应用公式向量$\overrightarrow{b}$在向量$\overrightarrow{a}$的方向上的投影|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\left|\overrightarrow{a}\right|}$求解.
解答 解:根据投影的定义可得:
向量$\overrightarrow{b}$在向量$\overrightarrow{a}$的方向上的投影|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\left|\overrightarrow{a}\right|}$=$\frac{-8+21}{\sqrt{{2}^{2}+{3}^{2}}}$=$\sqrt{13}$.
故选:B.
点评 本题主要考查向量投影的定义及求解的方法,公式与定义两者要灵活运用.解答关键在于要求熟练应用公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知x、y的取值如表所示:
若从散点图分析,y与x线性相关,且线性回归直线方程为$\widehat{y}$=0.95x+$\widehat{a}$,则$\widehat{a}$的值等于2.6.
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
5.已知正方形ABCD边长为$\sqrt{2}$,则|$\overrightarrow{AB}$+2$\overrightarrow{AC}$+$\overrightarrow{AD}$|=( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 6 |
10.求tan570°的值为( )
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
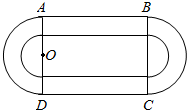 某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.