题目内容
【题目】某学习软件以数学知识为题目设置了一项闯关游戏,共有15关,每过一关可以得到一定的积分,现有三种积分方案供闯关者选择.方案一:每闯过一关均可获得40积分;方案二:闯过第一关可获得5积分,后面每关的积分都比前一关多5;方案三:闯过第一关可获得0.5积分,后面每关的积分都是前一关积分的2倍.若某关闯关失败则停止游戏,最终积分为闯过的各关的积分之和,设三种方案闯过n(![]() 且
且![]() )关后的积分之和分别为
)关后的积分之和分别为![]() ,要求闯关者在开始前要选择积分方案.
,要求闯关者在开始前要选择积分方案.
(1)求出![]() 的表达式;
的表达式;
(2)为获得尽量多的积分,如果你是一个闯关者,试分析这几种积分方案该如何选择?小明通过试验后觉得自己至少能闯过12关,则他应该选择第几种积分方案?
【答案】(1)![]() ;
;![]() ;
;![]() (2)见解析,小明应该选择方案三.
(2)见解析,小明应该选择方案三.
【解析】
(1)根据题意,分别得到各方案所对应的数列,从而得到![]() ;
;
(2)令![]() ,
,![]() 分别得到
分别得到![]() 的范围,结合题意中的
的范围,结合题意中的![]() ,从而做出判断.
,从而做出判断.
(1)按方案一闯过各关所得积分构成常数数列,故![]() ;
;
按方案二闯过各关所得积分构成首项为5,公差为5的等差数列,故![]() ;
;
按方案三闯过各关所得积分构成首项为![]() ,公比为2的等比数列,故
,公比为2的等比数列,故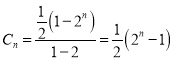 .
.
(2)令![]() ,即
,即![]() ,解得
,解得![]() ,
,
而当![]() 时,
时,![]() ,
,
又因为![]() 且
且![]() ,故
,故![]() 恒成立,
恒成立,
故方案二不予考虑.
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
故有,当![]() 时,
时,![]() ;当
;当![]() ,
,![]() ,
,
故当能闯过的关数小于10时,应选择方案一;
当能闯过的关数大于等于10时,应选择方案三.
小明应该选择方案三.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目