题目内容
【题目】已知椭圆![]() :
: ![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,
, ![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的面积为
的面积为![]() ,椭圆
,椭圆![]() 的离心力为
的离心力为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
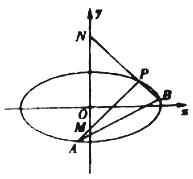
(Ⅱ)已知![]() 为坐标原点,直线
为坐标原点,直线![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
, ![]() 两个不同的点,若存在实数
两个不同的点,若存在实数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】(Ⅰ)根据题目条件,由椭圆焦点坐标和对称性计算![]() 的面积,建立等式关系,结合关系式
的面积,建立等式关系,结合关系式![]() ,离心率计算公式,问题可得解;(Ⅱ)由题意,可分直线是否过原点,对截距
,离心率计算公式,问题可得解;(Ⅱ)由题意,可分直线是否过原点,对截距![]() 进行分类讨论,再利用椭圆对称性、向量共线、直线与椭圆有交点等性质、条件进行运算即可.
进行分类讨论,再利用椭圆对称性、向量共线、直线与椭圆有交点等性质、条件进行运算即可.
试题解析:(Ⅰ)根据已知椭圆![]() 的焦距为
的焦距为![]() ,当
,当![]() 时,
时, ![]() ,
,
由题意![]() 的面积为
的面积为![]() ,
,
由已知得![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)若![]() ,则
,则![]() ,由椭圆的对称性得
,由椭圆的对称性得![]() ,即
,即![]() ,
,
∴![]() 能使
能使![]() 成立.
成立.
若![]() ,由
,由![]() ,得
,得![]() ,
,
因为![]() ,
, ![]() ,
, ![]() 共线,所以
共线,所以![]() ,解得
,解得![]() .
.
设![]() ,
, ![]() ,由
,由![]()
得![]() ,
,
由已知得![]() ,即
,即![]() ,
,
且![]() ,
, ![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,∴
,∴![]() ,
,
∴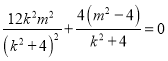 ,即
,即![]() .
.
当![]() 时,
时, ![]() 不成立,∴
不成立,∴![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,解得
,解得![]() 或
或![]() .
.
综上所述, ![]() 的取值范围为
的取值范围为![]() .
.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.